En esta página vamos recopilando todos los problemas que publicamos como Problemas de la Semana, y alguno más. Aquí sólo se incluyen los enunciados; cada problema está enlazado con la entrada del blog donde viene la solución.
Hemos cocinado un bizcocho rectangular, y sus medidas son de 30cm de largo por 10cm de ancho. Lo queremos cubrir con una servilleta cuadrada de papel que tiene 30 cm de diagonal, con lo cual quedan unos triángulos de bizcocho sin cubrir, como se ve en la figura. ¿Cuánto mide el área total de lo que queda sin cubrir? ¿Cuánto mide el área cubierta?
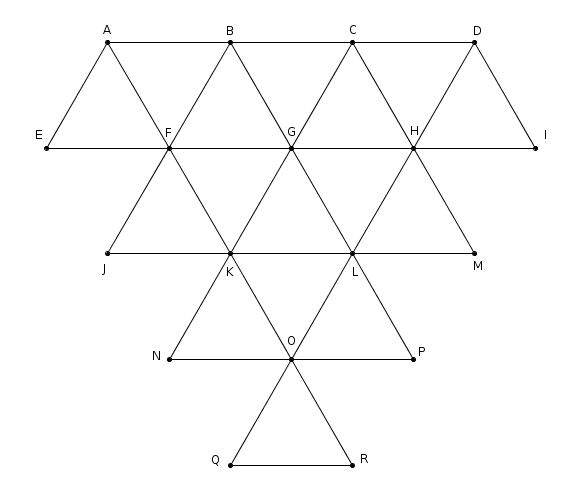
¿Sería capaz el lector de dibujar de un solo trazo el siguiente grafo lleno de triángulos?
¿Es usted capaz de dibujar, de un solo trazo, la siguiente figura triangulada?
1. Cuatro espías con trinchera se habían acomodado en asientos encarados.
2. Viajaban en el exprés de Pekín.
3. Dos iban junto a la ventanilla, y los otros dos al lado del pasillo.
4. La colocación resultaba un tanto extraña (como sin duda pensó el lector).
5. El espía inglés estaba sentado a la izquierda del señor B.
6. El señor A llevaba una trinchera beige.
7. El espía con trinchera de color oliva se hallaba a la derecha del espía alemán.
8. El señor C era el único que fumaba un puro.
9. El señor D estaba en frente del espía norteamericano.
10. El ruso, vestido de caqui, llevaba una bufanda al cuello.
11. El espía inglés miraba por la ventanilla, a su izquierda.
12. ¿Quién era el espía de la trinchera de color ocre?
¿A qué velocidad en kilómetros por hora crece una planta que en seis
meses ha pasado de tener 20 centímetros de altura a tener 30?
Encuentra un cuadrado que al sumarle dos se convierte en un cubo.
En cierto instituto, un profesor se ha quejado de que “la inmensa
mayoría del alumnado, quizás más del 75%, ha sacado una nota inferior a
la puntuación media del centro”.
¿Es esto posible? Si no lo es, razónalo. Si lo es, pon un ejemplo con una clase de 30 alumnos.
Un
chico debe lanzar con fuerza una pelota en línea recta para que,
después de rebotar en el suelo, siga en línea recta hasta colarse por
una pequeña ventana. Si la altura del chico es de 1'50 m, la altura de
la ventana es de 2'50 m y la distancia entre el chico y la pared donde
se encuentra la ventana es de 8 metros:
¿En qué punto del suelo debe hacer rebotar la pelota?
Si nos fijamos en la hora que marca el reloj, a la aguja horaria le
falta el triple de tiempo en llegar a las 6 que a la aguja de los
minutos.
¿Qué hora marca el reloj?
En una casa abandonada hemos encontrado una vieja caja fuerte cerrada. La cerradura se compone de cuatro rodillos, y en cada uno de ellos están 24 letras del alfabeto. Los rodillos han de combinarse de tal manera que formen una determinada palabra desconocida. Como queremos abrir la caja sin forzarla, hemos decidido ir probando con dichas letras todas las combinaciones posibles. Para probar cada combinación se invierten 6 segundos. Disponemos del fin de semana para encontrar la combinación correcta.
¿Tendremos suficiente tiempo?
Todas las personas que asistieron a una reunión se saludaron
estrechándose la mano. Uno de ellos se molestó en contar cuántos
apretones se habían dado y fueron 120.
¿Cuántas personas estuvieron en la reunión?
Un motorista viaja entre dos ciudades. El viaje de ida lo cubre a 90 km/h, y el de vuelta a 60 km/h.
¿Cuál ha sido la velocidad media de su recorrido?
(Ayuda: suponer que la distancia entre las ciudades es de 180 km)
Un
peluquero tiene dos botellas de agua oxigenada de un litro cada una. La
primera botella tiene agua oxigenada al 40% de concentración. La
concentración de la segunda botella es del 10%.
¿Cuánto tiene que mezclar de cada botella para que salga un litro de agua oxigenada con una concentración del 20%?
Tres matemáticos observaron que un conductor de un automóvil
infringía gravemente las normas de tráfico y se daba a la fuga. Todo fue
tan rápido que no pudieron anotar el número de la matrícula. Sin
embargo, el primer matemático se fijó en que las dos primeras cifras del
número eran iguales. El segundo matemático vio que las dos últimas
cifras del número también eran iguales, y el tercer matemático se fijó
que el número de cuatro cifras era un cuadrado perfecto.
¿Sabrías averiguar el número de la matrícula con estos datos?
Usando
solo cinco unos, sin emplear ningún signo de sumar, restar, multiplicar
o dividir, ¿cuál es la cantidad más elevada que puedes expresar?
Los alumnos y alumnas que se han graduado están de celebración. Han
organizado un baile; el cuadrado de la doceava parte ya han salido a la
pista, y el resto, 35, todavía están sentados charlando.
¿Cuántos alumnos se han graduado?
Tomamos tres parejas de números, 1-1, 2-2, 3-3, y las colocamos en el siguiente orden:
3 - 1 - 2 - 1 - 3 - 2
Podemos
darnos cuenta de que entre el 1 y el otro 1 hay un número, entre el 2 y
el otro 2 hay dos números, y entre el 3 y el otro 3 hay tres números.
¿Es
capaz el lector de ordenar las parejas 1-1, 2-2, 3-3, 4-4, siguiendo la
misma propiedad, es decir, que entre cada pareja haya exactamente la
cantidad de números que indica la propia pareja?
Cada
uno de los socios del Club VM es, o bien veraz, y dirá siempre la
verdad, o bien mentiroso y siempre responderá con una mentira. En mi
primera visita al club encontré a todos sus miembros, exclusivamente
hombres, sentados en torno a una gran mesa circular, almorzando. No
había forma de distinguir a veraces de mentirosos por su aspecto
externo, así que fui preguntándoles por turno si eran una u otra cosa.
De nada me sirvió, pues como era de esperar todos aseguraron ser
veraces. Volví a probar, esta vez preguntando a cada uno si su vecino de
la izquierda era veraz o mentiroso. Para sorpresa mía, todos
contestaron que el hombre sentado a su izquierda era mentiroso.
Más
tarde, de vuelta a casa, al pasar a limpio mis notas sobre el almuerzo
descubrí que había olvidado apuntar el número de personas sentadas a la
mesa. Telefoneé entonces al presidente del club, quien me informó que
eran 37. Después de colgar me di cuenta de que no podía confiar en esta
cifra, porque no sabía si el presidente era veraz o mentiroso. Decidí
entonces telefonear al secretario del club.
"No,
no", me contestó el secretario, "por desgracia nuestro presidente es un
mentiroso empedernido. La verdad es que estábamos cuarenta comensales."
¿A cuál de estos dos hombres debería yo creer?
Situados uno a cada orilla de un hermoso río tropical, y subidos en
lo más alto de dos enormes árboles, se encuentran dos pájaros que se
alimentan de pescado. De pronto aparece un pez en el río y los pájaros
se lanzan a cazarlo al mismo tiempo y con la misma velocidad. Los dos
pájaros alcanzan al pez al mismo tiempo. El río mide 70 metros de ancho y
los árboles tienen una altura de 30 y 40 metros respectivamente.
¿Sabrías encontrar en qué punto del río estaba el pez?
Nuestro televisor es de "40 pulgadas", esto quiere decir que la
diagonal de la pantalla mide 40 pulgadas. Además es panorámico: la
proporción entre sus lados o "relación de aspecto" es 16:9.
Intenta averiguar con estos datos la longitud de los lados en centímetros y el área de la pantalla en metros cuadrados.
Probar que si un número es primo, exceptuando el 2 y el 3, entonces el anterior o el siguiente es un múltiplo de 6.
A cierto profesor de matemáticas se le apareció un duende travieso
que le dijo: “estoy muy contento, porque a pesar de lo que dice el
Teorema de Fermat, he encontrado un número n, mayor que 2, que cumple
que
72n + 91n = 121n
Te reto a que adivines el número”.
“Eres un duende travieso y mentiroso” le contestó el profesor, “no puede existir ese número por una razón bastante sencilla”.
¿Eres capaz de encontrar una razón por la que, en este caso concreto, nunca se puede cumplir la igualdad para ningún n?
Tenemos un pentágono regular y desde un vértice cualquiera trazamos
las dos diagonales que parten de él. Estas dos diagonales, con los dos
lados que se juntan en el vértice, forman tres ángulos.
¿Son iguales estos tres ángulos? ¿Cuál es su medida?
(92) El jardín para pasear
En un jardín rectangular de 74 m de largo y 53 de ancho, hay dos paseos de cemento, perpendiculares y de 2 m de ancho.
¿Cuánto mide la superficie cultivable del jardín?
Encontrar
un número de tres cifras, A, B, C, tal que es igual a la suma de los
factoriales de dichas tres cifras, es decir, si el número es ABC,
entonces:
Elige un número cualquiera de tres cifras y escríbelo dos veces
seguidas para obtener un número de seis dígitos (por ejemplo 327, que se
convierte en 327327). Puedes comprobar que el número que resulta es
divisible por 7. Haz la división y comprueba que el cociente es
divisible por 11. Haz de nuevo la división y comprueba que el cociente
es divisible por 13.
¿Puedes explicar por qué ocurre esto con cualquier número que elijas?
(89) La pócima mágica
Un vendedor de feria está promocionando una "pócima mágica" que, según él, sirve para todo: crecepelo, antiarrugas, cortauñas... Actualmente tiene 150 litros de pócima, de los cuales el 7 por ciento es un producto químico que le cuesta dinero, y el resto es agua. Decide añadir más agua al producto para obtener más cantidad de pócima y así obtener más beneficios con la venta. Piensa: "Si disminuyo la concentración al 5 por ciento ganaré una pasta extra".
¿Cuánta agua tiene que añadir a sus existencias?
(88) La compra compartida
Cuatro
compañeros van hacia clase. Cada uno de ellos tiene que comprar una
cosa: una goma de 15 céntimos, un lápiz de 75 céntimos, un cuaderno de
3.75 euros y un libro de 18.75 euros. Después de comprar lo que hace
falta, a Paula le sobra 1 céntimo, a Juan 2 céntimos, a Luis 3 céntimos y
a Ana 4 céntimos. Si pasamos todo a céntimos, multiplicamos lo que se
ha gastado cada uno por lo que ha sobrado y sumamos los productos, se
obtiene 5490.
¿Qué objeto ha comprado cada uno de los cuatro?
(87) Celebración con langostinos
Dos amigos, que han acabado con éxito
los exámenes, deciden celebrarlo comiendo langostinos. Para ello, uno
compra 2 kg y el otro 3 kg. Cuando van a comérselos aparece un tercer
amigo que también quiere celebrar el fin de curso, y los otros dos
acceden a que los acompañe con la condición de que pague su parte
correspondiente, que asciende a 50 euros.
¿Cómo se repartirán esos 50 euros entre los dos primeros para que todos estén contribuyendo de forma equivalente?
(86) El cociente misterioso
Un
matemático tenía la costumbre de contestar a las preguntas poniendo
problemas. Un día le plantearon una división con más de cien cifras, y
le preguntaron cuál era el cociente. Después de un rato contestó: "Si en
esta división sumamos 6 al divisor y 72 al dividendo, no varían ni el
cociente ni el resto".
¿Cuánto vale el cociente?
(85) Musarañas comilonas
Comen tanto 17 osos como 170 monos, 100.000 musarañas tanto como 50 monos, y 4 elefantes comen lo mismo que 10 osos.
¿Cuántas musarañas serán necesarias para acabar con la comida de 12 elefantes?
(84) Los peregrinos
Ambrosio y Bonifacio son dos peregrinos que empiezan a caminar a
las 8 de la mañana del mismo día por una carretera en el mismo sentido.
Bonifacio lleva 28 kilómetros de ventaja, y ambos caminan cada día desde
las 8 de la mañana hasta las 8 de la tarde. Ambrosio camina con paso
regular 20 kilómetros el primer día, 18 el segundo, 16 el tercero y así
sucesivamente. Bonifacio camina con paso regular 4 kilómetros el primer
día, 8 el segundo, 12 el tercero, y así sucesivamente.
¿Cuándo y dónde se encontrarán?
(83) Los trabajadores enfermos
Cierta
empresa ha hecho una estadística de las enfermedades que han sufrido
sus trabajadores. El 84% enfermó de gripe, el 81% tuvo gastroenteritis, y
el 75% padeció ataques de alergia.
¿Qué porcentaje mínimo tuvo los tres tipos de dolencias?
(82) La merienda
Anteayer
fuimos a una cafetería, y pedimos una jarra de limonada, tres
bocadillos y siete magdalenas, y nos cobraron 12,30 euros. Ayer pedimos
en la misma cafetería una jarra de limonada, cuatro bocadillos y diez
magdalenas, y nos cobraron 15,50 euros. Hoy solo hemos pedido una jarra
de limonada, un bocadillo y una magdalena.
¿Cuánto nos cobrarán?
(81) Sacos por parejas
En
un almacén tenemos cinco sacos de trigo. El primer saco y el segundo
pesan juntos 11,5 kilos. El segundo y el tercero pesan juntos 13 kilos.
El tercero y el cuarto pesan juntos 15,5 kilos. El cuarto y el quinto
pesan 14,5 kilos, y el primero y el quinto pesan juntos 15,5 kilos.
¿Cuánto pesa cada saco por sí solo?
(80) El paseo en bicicleta
Dos
ciclistas salen a las 8 de la mañana y regresan a las 12. Durante ese
tiempo han recorrido un tramo llano a 30 kilómetros por hora, han subido
una colina a 20 km/h, la han bajado a 60 km/h y han regresado por el
mismo tramo llano a 30 km/h.
¿Cuál es la distancia total recorrida?
(79) Treinta
El número 30 es fácil expresarlo con tres cincos: 5 · 5 + 5.
¿Cómo se puede hacer esto mismo con otras tres cifras iguales?
(78) ¿Cuántos años tengo?
A un aficionado a los rompecabezas le preguntaron cuántos años tenía. La contestación fue compleja:
-Tomad
cuatro veces los años que tendré dentro de cuatro años, restadles
cuatro veces los años que tenía hace cuatro años y resultará exactamente
los años que tengo ahora.
¿Cuántos años tengo?
(77) Dos obreros camino del trabajo
Dos
obreros, uno viejo y otro joven, viven en un mismo apartamento y
trabajan en la misma fábrica. El joven va desde casa a la fábrica en 20
minutos; el viejo en 30 minutos.
¿En
cuántos minutos alcanzará el joven al viejo, andando ambos a su paso
normal, si éste sale de casa 5 minutos antes que el joven?
(76) Caminando por el ecuador
Si pudiéramos recorrer la Tierra siguiendo el ecuador, la coronilla de nuestra cabeza describiría una línea más larga que la planta de los pies.
¿Qué magnitud tendría la diferencia entre estas longitudes?
(75) División por 11
Tomamos las cifras 1, 2, 3, 4, 5, 6, 7, 8, 9. Encuentra el número más grande que se puede escribir con estas nueve cifras, sin repetir ninguna, y que sea divisible por 11.
(74) El radio desconocido
Averigua la longitud del radio de la circunferencia que aparece en el gráfico adjunto:
(73) El pastor ingenioso
Había un pastor que sólo sabía contar hasta diez y tenía a su cargo un rebaño numeroso. Para saber si le faltaba alguna oveja, inventó un sistema que ponía en práctica todos los días a la caída de la tarde. Agrupaba a sus animales de dos en dos, luego de tres en tres, después de cuatro en cuatro, más tarde de cinco en cinco y, por último, de seis en seis: en todos los casos le sobraba una oveja. Las agrupaba entonces de siete en siete, y todos los grupos le quedaban con idéntica cantidad de ovejas.
¿De cuántas ovejas se componía el rebaño?
(72) Seguro de Vida
Teresa echó una mirada sobre el hombro de su hijo.
-¡Eh, esos son los papeles de mi seguro de vida! -exclamó ella-. No me digas que ha vencido.
-No, mamá. Sólo que descubrí una curiosidad en el número de la póliza -dijo el muchacho-. Es el menor número con una raíz cúbica y una raíz séptima diferentes y enteras.
¿Cuál es el número?
(71) Un Caso de Identificación
-Me crucé con uno sólo de ellos -dijo Marta-. Con el de barba. ¿Cómo se llama?
-Veamos -contestó Carlos-. Dos de ellos están casados, dos tienen los ojos azules. El único de los tres que lleva barba tiene ojos marrones. La mujer de Daniel es la hermana de Camilo, y el soltero tiene el mismo color de ojos que Javier.
¿Quién es el barbudo?
-¿Recuerdas aquella noche fría del año pasado, la primera verdadera nevada en muchos años? -preguntó Tony-. Tú querías que condujera hasta el centro.
-No lo hiciste, y por eso nos perdimos una buena fiesta -replicó Nina-. No lo olvido. ¿Qué temperatura hacía?
-Una temperatura bastante curiosa -respondió su marido después de pensarlo-. El número de grados Fahrenheit y el de grados Celsius terminaban ambos en 5.
¿Qué valores son esos?
Las dos ancianas habían estado contándose chismes de amigos y conocidos, hasta que finalmente acabaron hablando de dos jóvenes parientes.
-Guillermo se casó con Juliana, y Daniel con Elizabeth -declaró una de ellas.
-No, no -discrepó la otra-; Guillermo se casó con María, y Daniel con Juliana.
De hecho, ninguna de las ancianas estaba totalmente errada.
Entonces, ¿quién se casó con quién?
–Me alegro por tus amigos, pero ese sitio al que fuisteis me parece demasiado caro –dijo Carina–; ¿cuánto te costó?
–Vamos –dijo Fernando con una sonrisa–, sabes que se trataba de nuestra reunión anual. La cena sólo costó 99.97 euros, de modo que pudimos dividir la cuenta en partes exactamente iguales entre todos.
¿Cuánto le costó la cena a Fernando, y cuántos amigos eran en la reunión?
(67) Negocios con trampa
Te ofrecen un par de negocios. En el primero vas a ganar 10 € el primer día, 20 € el segundo día, 30 € el tercer día, y así sucesivamente hasta llegar al día 15. En el segundo ganas 0.10 € el primer día, 0.20 € el segundo día, 0.40 € el tercer día, 0.80 € el cuarto día, y así sucesivamente hasta el día 15.
Si te ofrecen escoger entre uno de los dos negocios, ¿con cuál te quedarías?
(66) Las zanahorias
Un conejo tiene un número de zanahorias en su jaula. Cada día se come un cuarto de las zanahorias que le quedan. Después de cuatro días se ha comido 350 zanahorias.
¿Cuántas zanahorias había al comienzo?
(65) Venta de coches
El beneficio de un vendedor de coches ha sido de 21.000 euros, después de haber vendido un cierto número de coches, todos al mismo precio. Si hubiera vendido un coche más y recibido 100 euros menos por cada coche, habría obtenido el mismo beneficio.
¿Cuántos coches se vendieron, y cuál fue el precio de cada uno?
Miriam tarda 4 minutos y 17 segundos en preparar un helado.
Trabajando al mismo ritmo, ¿cuánto necesitaría para completar su encargo diario de 60 helados?
Imagina un ser (extraterrestre) que emprende una carrera, y que en cada paso emplea un segundo de tiempo, pero el primer paso es de 1 metro de longitud, el segundo de 2 metros, el tercero de 4 metros, y así sucesivamente, tardando un segundo en cada paso y doblando en cada paso la longitud del paso anterior.
¿Será capaz de superar a Usain Bolt que corrió 100 metros en 9,56 segundos? ¿Y cuánto tardará en hacer la distancia de Granada a Madrid, que es aproximadamente de 420 kilómetros?
Observa el reloj digital formado por los 10 dígitos que dan las horas, los minutos, el día, el mes y el año. El día 26 de abril de 1995, a las 17 horas y 38 minutos, el reloj marcaba la fecha y la hora usando exactamente los diez primeros números naturales (0-9), ninguno de ellos repetido, como muestra el siguiente esquema:
17 : 38 26 – 04 – 95
¿Cuándo se produjo o se producirá por primera vez esta situación en el siglo XXI?
Un recipiente lleno de agua pesa 35 kilos. Cuando sólo está lleno hasta la mitad, pesa 19 kilos.
¿Cuánto pesa el recipiente vacío?
Tenemos tres cajas etiquetadas con frases que hacen referencia a su contenido. La primera caja tiene una etiqueta que dice “el oro está aquí”. La frase de la segunda caja es “el oro no está aquí”. En la tercera caja pone “el oro está en la primera caja”. Sólo una de las tres frases es verdadera, las otras dos son falsas.
¿Puedes averiguar dónde está el oro?
Tenemos 5 montones de monedas, uno de los cuales está compuesto íntegramente por monedas falsas. Sabemos que cada moneda auténtica pesa 10 gramos y que cada moneda falsa pesa 9 gramos. Tenemos también una báscula electrónica que proporciona el peso con una precisión absoluta.
¿Cómo podemos saber qué montón es el que contiene las monedas falsas realizando el mínimo número de mediciones? ¿Cuál es este número de mediciones?
A medio camino en un vuelo transatlántico, una saca de correo se cae de la parte de atrás del avión. Al mismo tiempo, una de las ruedas del tren de aterrizaje se separa y cae también verticalmente.
¿Cuál será, la saca o la rueda, la que primero se estrelle contra el suelo?
¿Cuánto es la mitad de dos tercios de tres cuartos de cuatro quintos de cinco sextos de 48?
(56) Vida futura
Una vidente predice que morirá a los 99 años. En este momento, según su predicción, dos tercios de su vida pasada es igual a cuatro quintos de su vida futura.
¿Cuál es su edad actual?
(55) Repartamos beneficios
Sara tiene que repartir las ganancias de la lotería, que han sido exactamente 8268 €, entre todos los miembros de una peña de juego. Incluyéndose ella misma, sabemos que hay entre 80 y 150 miembros en la peña.
Si Sara logra repartir los beneficios en euros enteros (sin tener que usar céntimos), de forma exacta e igual para todos:
¿Cuántos miembros tiene la peña? ¿Cuánto gana cada uno?
(54) Competición de tiro
Dos hermanos participan en una competición de tiro con escopetas de aire comprimido. Daniel dispara 5 perdigones en 10 segundos, mientras que en otra prueba Dennis dispara 10 perdigones en 20 segundos.
¿Cuál de los dos hermanos es más rápido cargando la escopeta?
(53) Obtén el cien
¿Cómo podemos obtener el número 100 usando todas las cifras del 1 al 9 una sola vez, y sólo con los signos +, −, × y los paréntesis adecuados?
Nota: hay varias maneras diferentes de conseguirlo.
(52) Un león a punto de comer
El príncipe del país de las matemáticas se encuentra frente a tres puertas de un gran castillo. Detrás de una puerta hay un león hambriento. Detrás de otra no hay nada, y detrás de la tercera hay una princesa. En la puerta de la izquierda pone: “Aquí está el león”. En la puerta del centro pone: “Aquí está la princesa”. En la puerta de la derecha pone: “Aquí no está el león”. Pero el paje del príncipe le avisa de una cosa: ¡Alerta, príncipe, sólo uno de los carteles es falso!
¿Qué tiene que hacer el príncipe para reunirse con la princesa sin ser devorado por el león?
Dos amigos que tienen una jarra de 8 litros de vino lo quieren repartir en 2 partes iguales. Disponen también de dos jarras vacías de 5 y 3 litros respectivamente.
La pregunta es clara, ¿cómo pueden repartirse el vino en 2 partes iguales sin tirar nada?
Dos pececitos están juntos y empiezan a nadar. Nadan 6 metros en línea recta y luego ambos giran 90º a la derecha, nadando cada uno en línea recta 8 metros más.
¿Cuál puede ser la mayor distancia que los separa ahora?
Una cuerda de 40 metros de longitud tiene sus extremos atados a la parte superior de dos palos de 22 metros de altura. Si la cuerda cuelga a 2 metros del suelo:
¿Cuál es la separación entre los dos palos?
La señora Menchu, una gran fumadora durante muchos años, finalmente decidió dejar de fumar al enterarse de la malignidad del tabaco y ver que todos sus amigos y amigas estaban dejándolo ya. “Acabaré los 27 cigarrillos que quedan”, se dijo, “y jamás volveré a fumar”. La costumbre de la señora Menchu era fumar exactamente 2/3 de cada cigarrillo. No tardó mucho en descubrir que con la ayuda de una cinta engomada podía pegar tres colillas y hacer otro cigarrillo.
Con 27 cigarrillos, ¿cuántos puede fumar antes de abandonar el tabaco para siempre?
(47) Fechas españolas y americanas
En España, fechas como 6 de diciembre de 2010 suelen abreviarse 6/12/10, pero en otros países como Estados Unidos, se da primero el mes y luego el día, escribiéndose 12/6/10.
Si desconociésemos cuál de ambos sistemas se ha utilizado, ¿cuántas fechas quedarían indeterminadas en la notación abreviada?
Mauricio, el bisabuelo de José, no es ciertamente centenario, pero sí de edad muy avanzada. Podemos decir que el año anterior, su edad era múltiplo de 8, y que el año próximo es múltiplo de 7.
¿Cuántos años tiene Mauricio?
En cierto libro nos ha aparecido una operación bastante larga:
999 – 998 + 997 – 996 + 995 – 994 + … + 5 – 4 + 3 – 2 + 1
Es decir, se trata de ir sumando y restando los números, en sucesión decreciente, desde el 999 hasta el 1, los impares se suman, los pares se restan.
¿Eres capaz de calcular esta operación?
Algunos números pueden tener muchas cifras decimales, incluso infinitas. Considera el número decimal
0’012345670123456701234567…
Si te fijas verás que los decimales se van repitiendo en una sucesión muy fácil. Observa que la primera cifra decimal es un 0, la segunda un 1, la tercera un 2, etc., y si sigues contando, la cifra que está, por ejemplo, en el lugar décimo es un 1, y la cifra que está en el lugar vigésimo es un 3.
¿Sabrías decir qué cifra decimal está en el lugar milésimo?
Observa los dos rectángulos de la figura.
¿Cuál de los dos ocupa mayor superficie, el ABCD ó el BEFD? Razona tu respuesta.
La pirámide del gráfico está formada por ladrillos, cada uno con un número. El número de cada ladrillo es igual a la suma de los dos ladrillos sobre los que se apoya. Averigua los números que faltan. (Pista: comienza por averiguar razonadamente el número contenido en el ladrillo marcado con una “x”)
Este es el mensaje que Hugo ha mandado a Mario. Para que nadie se entere de lo que pone, lo ha cifrado usando un alfabeto desplazado, es decir, cada letra ha sido sustituida por otra desplazando el alfabeto un número concreto de lugares. De este modo ha creado un criptograma: WHPJR ÑD FRPWUDVHQD SDUD HPWUDU HP HÑ RUGHPDGRU GH MXDP. El problema es que Hugo ha olvidado dar a Mario el número que indica los lugares que ha desplazado las letras del abecedario.
¿Eres capaz de descifrar el mensaje?
A Felipe y Margarita les gusta competir con sus calculadoras. Al igual que muchas otras potencias, 759 no cabe en la pantalla, pero Felipe afirma que el resultado acaba en 1, mientras que Margarita piensa que acaba en 43.
¿Cuál de los dos tiene razón?
El abuelo de Dani, que es un simpático señor que ya cumplió los 70 pero al que aun le falta para llegar a los 80, y el padre de Laura, que es cuarentón, viven en la misma calle, en la acera de los pares y en casas contiguas. Laura observa que el producto de la edad de su padre por el número de la casa del portal en que vive es igual al producto de la edad del abuelo de Dani por el número de su portal.
Calcula las edades de ambos y los números de sus casas.
Tenemos un profesor de matemáticas que no pierde oportunidad de ponernos problemas. El otro día hicimos un examen y hoy, en la clase, le dijimos que si lo había corregido. Nos dijo que sí, pero que los había olvidado en su casa. Nos fastidió, así que le preguntamos si recordaba al menos el número de aprobados. Nos contestó que no recordaba el número exactamente, pero que le llamó la atención que al 95% de los alumnos y alumnas que habían aprobado les gustase mucho el baloncesto. Si en clase hay 35 alumnos/as:
¿Cuántos aprobaron?
(37) Cuadrado al cuadrado y algo más
He tomado un determinado número y hallado su cuadrado. Después, he elevado este cuadrado al cuadrado y multiplicado el resultado por el número original. Al final de mis cálculos, hallo como resultado un número de 7 cifras acabado en 7.
¿Cuál es el número original?
(36) Sumas de impares
Nos han encargado que sumemos todos los números impares desde el 1 al 101 ambos inclusive. Después de un buen rato hemos finalizado la cuenta, pero luego nos han encargado la suma del 1 al 201, y cansados de sumar, queremos encontrar una fórmula fácil que nos dé el resultado.
Encuentra la fórmula, y como aplicación calcula la suma de los impares desde el 1 al 101, del 1 al 201 y del 1 al 343.
(35) El cuadrado maya de la buena suerte
En una pirámide maya hay un grabado como el que reproducimos. Debajo de él se puede leer: “Aquel que calcule la superficie del cuadrado interior, sabiendo que el exterior mide 100 centímetros cuadrados, recibirá del dios Itzamná suerte durante 50 años del calendario Tzolkin”. Si crees en la fuerza del destino, ponte a trabajar.
(34) Una calculadora estropeada
Imagina que tu calculadora tiene estropeada la tecla del "cero". El juego consiste en conseguir que aparezcan en la pantalla estos números: 250, 205, 2050, 0'025.
¿Y cómo se podrían efectuar los siguientes cálculos? 0'025 · 205; 2050 : 250.
Recuerda que la tecla del "cero" sigue estropeada.
(33) Llenas, medio llenas y vacías
Tres hermanos recibieron 21 botellas cerradas iguales con diferentes cantidades de un refresco de naranja: 7 estaban llenas; otras 7, medio llenas, y las 7 restantes, vacías.
¿Cómo repartirse las 21 botellas de modo que cada uno reciba el mismo número de botellas y la misma cantidad de refresco sin destapar las botellas?
(32) Los güisquis
Un escocés y medio se bebe un güisqui y medio en un día y medio.
¿Cuántos güisquis se beben seis escoceses en seis días?
(31) Las cuatro tarjetas
Tenemos cuatro tarjetas blancas. Por el otro lado son todas azules. Hay que dar la vuelta a las tarjetas para que queden todas mostrando su lado azul, pero en cada movimiento se le debe dar la vuelta obligatoriamente a tres (y sólo tres) tarjetas a la vez.
¿Cómo conseguirlo?
(30) El jardín
Un jardín cuadrado tiene a lo largo de tres de sus lados una valla sostenida por 28 postes espaciados entre sí 2 m.
Si hay un poste en cada una de las esquinas, ¿Cuál es el área del jardín?
(29) Medias semanales
Bartolomé es vendedor ambulante seis días a la semana. Ayer, viernes, calculó que durante esta semana había conseguido una ganancia media de 48 euros diarios. Sin embargo, al hacer la misma cuenta hoy, sábado, resulta una media de 60 euros diarios.
¿Cuánto ha ganado hoy?
Un antropólogo llegó a la isla de los mentirosos y de los veraces, en la que viven dos clases de habitantes: los que siempre mienten (mentirosos) y los que siempre dicen la verdad (veraces).
Se encontró con tres nativos, Abel, Beto y Carlos. Se dirigió a Abel y le preguntó: "¿Son Beto y Carlos ambos veraces?". Abel respondió que sí.
Entonces le volvió a preguntar: "¿Beto es veraz?". ¡Para su sorpresa, Abel respondió que no!
¿Se puede determinar quién es veraz y quién es mentiroso?
(27) Criptosuma
Las criptosumas son sumas en clave. Cada cifra ha sido reemplazada por una letra diferente: a igual letra corresponde la misma cifra. Nunca un número comienza por cero.
¿Qué suma se oculta en la siguiente criptosuma?
(26) División en cuatro trozos
Nos han dado una plancha de madera con la forma que tiene la figura (un rectángulo al que le falta la cuarta parte). Debemos partirla en cuatro trozos exactamente iguales.
¿Cómo podemos hacerlo?
(25) La casa encantada
En una casa encantada hay un fantasma bastante especial: aparece en cuanto el reloj comienza a dar la medianoche y desaparece con la última campanada. El reloj tarda seis segundos en dar seis campanadas.
¿Cuánto dura la aparición del fantasma?
(24) Iván el perezoso y el diablo
Según un antiguo cuento ruso, Iván el perezoso se hallaba un día holgazaneando a orillas de un río.
—Todo el mundo me dice que busque un trabajo o me vaya al diablo —suspiró—. No creo que ninguna de las dos cosas me ayude a hacerme rico.
Tan pronto como dijo esto, apareció el diablo en persona.
—¿Quieres ganar dinero, Iván? —le preguntó.
Iván asintió perezosamente con la cabeza.
—Muy bien —continuó el diablo—. ¿Ves ese puente? Pues todo lo que tienes que hacer es cruzarlo. Cada vez que lo hagas, se doblará el valor del dinero que llevas en el bolsillo.
Iván se dirigía ya hacia el puente, cuando el diablo le detuvo.
—Un momento —le dijo astutamente—. Puesto que me he mostrado tan generoso contigo, creo que me merezco una pequeña recompensa por mis esfuerzos. ¿Querrás darme ocho rublos cada vez que cruces el puente?
Iván el perezoso se apresuró a asentir. Cruzó el puente y metió la mano en el bolsillo. Su dinero se había doblado por arte de magia... Le lanzó los ocho rublos al diablo, que permanecía al otro lado del río y cruzó de nuevo. Otra vez se dobló su dinero. Le pagó otros ocho rublos al diablo y cruzó por tercera vez. Y el dinero se dobló también. Pero al contarlo, descubrió que no le quedaban más que ocho rublos en el bolsillo, que tuvo que entregar al diablo, con lo cual se quedó sin dinero que doblar.
El diablo soltó una carcajada y desapareció.
¿Cuánto dinero tenía Iván el perezoso en el bolsillo al principio?
El problema de los cuatro cuatros consiste en obtener todos los números que se puedan con cuatro cuatros (ni uno más, ni uno menos) y las reglas de las operaciones aritméticas básicas. Concretando más, debemos encontrar la manera de escribir todos los números del cero al diez utilizando cuatro cuatros, los signos de sumar, restar, multiplicar y dividir, y los paréntesis.
Hay que tener en cuenta que para cada número puede haber varias formas de hacerlo. Como ejemplo, damos la obtención del cero:
0 = 4 + 4 − 4 − 4; o bien, 0 = 44 − 44
1 = ...
2 = ...
etc.
(22) Cuadrados correlativos
Obsérvese las siguientes igualdades (se puede comprobar que son ciertas):
32 + 42 = 52
102 + 112 + 122 = 132 + 142
212 + 222 + 232 + 242 = 252 + 262 + 272
Como ya se habrá dado cuenta, en cada igualdad los números van correlativos. ¿Sería capaz de encontrar otra igualdad como las anteriores pero con cinco sumandos en el primer término y cuatro en el segundo? Es decir, buscar una expresión:
a2 + b2 + c2 + d2 + e2 = f2 + g2 + h2 + i2
siendo a, b, c, d, e, f, g, h, i, números enteros consecutivos.
(21) El número de teléfono
Cuando le pregunté el número de teléfono a un compañero, me dijo:
"Mi número tiene cinco cifras. Si le pones un 4 delante obtienes un número que es el cuádruple del que obtienes si le pones el 4 detrás."
¿Cuál es el número de teléfono de mi compañero?
Algunas parejas de números primos se diferencian en 2 unidades. Diremos entonces que estos números son primos gemelos.
El número que hay entre los 2 números de cada pareja de primos gemelos tiene una curiosa propiedad: es un múltiplo de 6 (exceptuando la primera pareja de primos gemelos: 3 y 5).
Trate de dar una explicación convincente de esta propiedad.
(19) Las patatas fritas
Tres viajeros se detienen en un bar para cenar, pero el cocinero sólo puede ofrecerles patatas fritas. Los viajeros se duermen agotados. Uno de ellos se despierta, se come la tercera parte de las patatas y se vuelve a dormir. Al poco se despierta otro, que se come la tercera parte de las patatas restantes. El tercero hace lo mismo. El cocinero vuelve a la mesa y se encuentra a los tres viajeros dormidos y ocho patatas en el plato.
¿Cuántas había al principio?
Antonio me comentaba el otro día: anteayer tenía 22 años, pero el año próximo tendré 25.
¿Cuándo es mi cumpleaños?
(17) El concurso de música
En un concurso de música han acudido siete participantes, y el jurado ha decidido que participen en el siguiente orden: Dolores Pérez, Remedios García, Miranda Fernández, Fátima Rosales, Soledad Moreno, Laura Martín, Silvia Hermosillo.
Las concursantes aceptan el orden de participación pero se preguntan el porqué de dicho orden.
¿Sabrías tú dar una razón lógica de por qué el jurado ha decidido que participen en dicho orden?
(16) El papel doblado como una malla hexagonal
Este problema trata de tomar un folio o una cuartilla de papel, y sin ayuda de ningún medio exterior, tan solo con las manos, doblarlo de forma que los dobleces aparezcan formando una especie de malla hexagonal, igual que las de algunas alambradas, como en la ilustración:
(15) Los Relojes
En el mismo instante, el reloj A marca las cinco y el reloj B marca las siete. A adelanta un minuto cada hora y B retrasa 2 minutos cada hora.
¿En cuánto tiempo marcarán la misma hora por primera vez?
¿Cuál es la hora común que marcarán en ese momento?
¿Cuántas veces coincidirán marcando la misma hora en un año?
(14) Rutas posibles
¿De cuántas maneras puedo ir de A hasta B por las líneas, si sólo se puede ir de arriba a abajo y de izquierda a derecha?
(13) El cuadrado aparecido
Como se puede apreciar en la ilustración, tenemos un cuadrado que hemos dividido en varias piezas de diversos colores. Obsérvese que el cuadrado ocupa 64 cuadraditos más pequeños (8×8).
Hemos dispuesto las piezas de colores de otra manera, formando ahora un rectángulo, en el que hay 65 cuadraditos (5
×
13) en total. De repente ha aparecido un cuadradito más pero los dibujos de las piezas son los mismos, ¿o no?
¿Por qué hay un cuadradito más en este nuevo dibujo que en el de arriba?
El triángulo exterior de la figura es equilátero y su área es de 4 metros cuadrados. Los triángulos interiores se han construido uniendo los puntos medios de los lados. Calcula el área de la zona sombreada.
¿Qué altura tiene un tronco que es 2 metros más corto que un árbol de altura triple que la del tronco?
¿En qué orden están los siguientes números? 5 - 4 - 2 - 9 - 8 - 6 - 7 - 3 - 1
Un pastor que lleva una oveja, un lobo y una col, quiere cruzar un río. Para ello dispone de una barca en la que sólo caben dos, el pastor y algo más. Pero al cruzar con la barca, si deja solos al lobo con la oveja, el lobo se comerá a la oveja, y si deja a solas la oveja con la col, la oveja se comerá a la col.
¿Cómo debe proceder para cruzar el río y que lleguen todos sanos y salvos a la otra orilla?
Un pastelero recibe tres cajas opacas. Una caja contiene caramelos de menta, otra caramelos de anís, y otra un surtido de caramelos de menta y de anís. Las cajas tienen etiquetas que ponen "caramelos de menta" "caramelos de anís" o "mezclados", pero el pastelero recibe el aviso de que todas las cajas están mal etiquetadas.
¿Cuántos caramelos necesita sacar el pastelero para verificar el contenido de las cajas?
¿Cómo se descifra el siguiente código de 169 dígitos? 000000000000000111111111000111111111110 0111111111110011000100011001100010001100111110111110011110001111000111111111000001010101000000110101100000011111110000000000000000
En el interior de una habitación herméticamente cerrada hay una bombilla, y fuera de la habitación hay tres interruptores. Sólo uno de los tres enciende la bombilla. Mientras la puerta esté cerrada puedes pulsar los interruptores las veces que quieras, pero al abrir la puerta debes decir cuál de los tres interruptores enciende la bombilla.
¿Cómo resolver el problema?
¿Cómo se puede cronometrar un tiempo de nueve minutos utilizando dos relojes de arena, uno de cuatro minutos y otro de siete?
Un alumno le pregunta a un profesor "¿Qué edad tienen tus tres hijas?", y el profesor contesta "Si multiplicas sus edades da 36, y si las sumas da el número de tu casa"; "me falta un dato", contesta el alumno, y el profesor le responde "es verdad, la mayor toca el piano".
¿Qué edades tienen?
En la Tierra Falsa todos los habitantes mienten siempre. En la Tierra Cierta todos los habitantes siempre dicen la verdad. Un extranjero se encuentra atrapado en una habitación que tiene dos puertas. Una puerta lleva a la libertad y la otra no. Las puertas están custodiadas por un carcelero de la Tierra Falsa y otro de la Tierra Cierta. Para dar con la puerta que lleva a la libertad el extranjero puede hacer sólo una pregunta a uno de los dos carceleros, pero no sabe cuál es el de la Tierra Falsa y cuál el de la Tierra Cierta.
¿Qué pregunta formuló?
Soy de tres cifras.
Si mi 4 fuera un 9,
Y mi 6 fuera un 3,
Lo que ahora soy valdría
Uno menos que la mitad
De lo que entonces sería.
¿Qué número soy?
Un miércoles noche en el living del señor Yani Puf. En verdad, de living ya no le iba a servir más, pues esa misma mañana había sido limpiamente asesinado. Con tal motivo, el gran investigador Tom Bola había reunido a los seis sospechosos. Cada uno de ellos solía visitar al señor Puf un día distinto y fijo de la semana. Únicamente el domingo Yani Puf no recibía visitas.
Esto es lo que declararon cada uno de los sospechosos cuando Tom Bola los interrogó:
El deshollinador: "yo venía a limpiarle la chimenea dos días después del pintor".
El tenista: "yo lo visitaba dos días después que el violinista".
La secretaria: "yo lo venía a ver dos días después que el tenista".
El pintor: "yo venía a pintarlo dos días después que ella".
El violinista no dijo nada.
El jinete: "yo venía a visitarlo dos días después que el deshollinador".
El gran investigador Tom Bola comprobó que todos habían dicho la verdad.
Según esto, ¿cuál de los sospechosos visitaba a Yani Puf los miércoles, y por tanto era el asesino?
Estos problemas han sido extraídos de las siguientes fuentes y libros:
-De la revista Selecciones del Reader's Digest.
-Del libro Matemágicas, de Ignacio Soret Los Santos.
-Del libro Enigmas para Darle al Coco, de Àngels Navarro.
-Del libro Álgebra Recreativa, de Yakob Perelman.
-Del libro Festival Mágico-Matemático, de Martin Gardner.
-Del libro
Problemas a mí 1, de Fernando Corbalán y José María Gairín.
-Del libro
Un cuento enmarañado y otros problemas de almohada, de Lewis Carroll.
-De la web
Problemas de Geometría realizada por Jesús Escudero Martín.
-Del libro
Matemáticas Recreativas, de Yakob Perelman.
-Del libro
Situaciones problemáticas de Jaime Poniachik.
-Del libro
El país de las mates, 100 problemas de ingenio 1,
de Miquel Capó Dolz.
-Del libro The Riddles of the Sphinx, de David J. Bodycombe, Penguin Books.
-Del libro Ruedas, vida y otras diversiones matemáticas, de Martin Gardner.
-Del libro Rosquillas anudadas y otras amenidades matemáticas, de Martin Gardner.
-De los libros de texto de matemáticas de 3º y 4º ESO (edición 2010) de la editorial Anaya.
-De los libros de texto de matemáticas de 3º y 4º ESO (edición 2010) de la editorial SM.
-Del libro El Mentor de Matemáticas, editorial Océano.
-Del Calendario Matemático, con problemas seleccionados por Marisa Fernández Villanueva y publicado en 2008 por la editorial SM.
-De la película La Habitación de Fermat.

















No hay comentarios:
Publicar un comentario