[El Problema de la Semana] Más Triángulos de un Solo Trazo

Continuando con el trazado de grafos sin levantar el lápiz del papel, proponemos al lector el siguiente:

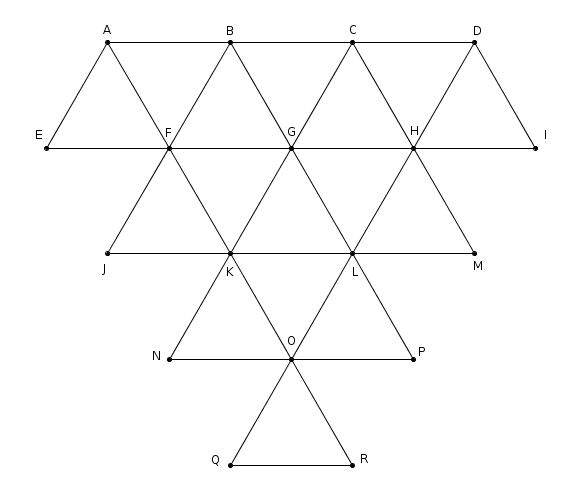
¿Sería capaz el lector de dibujar de un solo trazo el siguiente grafo lleno de triángulos?

Más abajo encontrará la solución.

Esta fotografía está tomada en el Centro de Conferencias KAFD en Riyadh, Arabia Saudita. El autor del diseño es Daniel Buren, un artista conceptual francés. La imagen está sacada de este sitio.

SOLUCIÓN:

El recorrido se puede hacer de muchas formas. A continuación exponemos una de las posibles soluciones, la cual me fue sugerida por un grumete del Barco Escuela:

A-E-F-J-K-N-O-Q-R-O-K-F-A-B-F-G-K-L-O-P-L-G-B-C-G-H-L-M-H-C-D-H-I-D

También exponemos otra solución, con un recorrido un poco más complejo:

A-E-F-G-H-I-D-H-L-O-Q-R-O-K-F-A-B-C-G-K-N-O-P-L-G-B-F-J-K-L-M-H-C-D

 

AMPLIACIÓN:

Como se ha explicado en el problema de la semana anterior, Triángulos de un Solo Trazo, Euler demostró que un grafo era resoluble mediante un solo trazo siempre que el número de vértices impares fuera cero o dos, pero no es resoluble si el número de vértices impares es cuatro o más.

En nuestro ejemplo de hoy tenemos que todos los vértices son pares, salvo el A y el D. Luego este grafo es resoluble, siempre que tomemos A y D como puntos de inicio y final.

Nota: este problema está inspirado en uno de los capítulos del libro Mathematics and the Imagination, de Edward Kasner y James Newman.