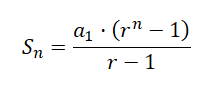[El Problema de la Semana] Cinco unos

Un problema en el que solo empleamos cinco palitos:

Usando solo cinco unos, sin emplear ningún signo de sumar, restar, multiplicar o dividir, ¿cuál es la cantidad más elevada que puedes expresar?

La respuesta al problema, cinco giros de rueda más abajo.

Los unos son números altos y delgados, y ¿qué deportistas son los más altos? Aquí tenemos a cinco "unos" = ases en el baloncesto de la NBA de todos los tiempos: de izquierda a derecha, Magic Johnson, LeBron James, Michael Jordan, Wilt Chamberlain (que sigue ostentando el récord de 100 puntos en un solo partido) y Larry Bird. Lo curioso es que los números de las camisetas son muy parecidos entre sí, y abundan en el dígito 3.

SOLUCIÓN:

Se trata de un problema en el que lo único que podemos usar son las potencias, y distribuir nuestros cinco unos entre la base y el exponente. Con que pensemos un poco vemos que los números más altos pueden salir de elevar 111 a 11 y de elevar 11 a 111.

Hacemos los cálculos con ayuda de la calculadora web2.0calc:

111¹¹ =  31517572945366073781711

11¹¹¹ = 3.93 · 10¹¹⁵ aproximadamente; su valor exacto es:

39317695287172535490534173386882756704761607664135852855034678556753487133293648186980649622260361388994869790176611

Se ve claramente que 11¹¹¹, que sale bastante mayor que un gúgol, es muy superior a 111¹¹, que no llega al orden de los cuatrillones.

Nota: este problema ha sido adaptado del libro: Álgebra Recreativa, de Yakob Perelman.

Otra leyenda sobre el tablero de ajedrez

Cuaderno de bitácora: he estado leyendo recientemente el libro Tradiciones y Leyendas Sevillanas, de José María de Mena, publicado por Plaza y Janés en los años 80 del siglo pasado, y me he encontrado con una versión alternativa de la leyenda sobre el tablero de ajedrez. Esta versión se centra en el siglo XI, y los protagonistas son el moro Abenamar, poeta, visir y amigo del rey Almotamid, y el rey castellano Alfonso VI.

Figura 1

Transcribimos a continuación la leyenda, tal y como la narra José María de Mena:

De cómo Abenamar salvó a Sevilla

El poderoso rey Alfonso VI de Castilla, en su juventud, siendo príncipe, perseguido por su hermano usurpador del reino, hubo de refugiarse en la corte árabe de Toledo, en la que dedicado a forzosa ociosidad, se entretuvo en aprender el noble juego del ajedrez.

Muerto el usurpador, y exaltado al trono don Alfonso tras la jura de Santa Gadea, en Burgos, se propuso ensanchar el reino castellano, a cuyo efecto conquistó Toledo, y cruzando después la línea del Tajo hizo incursiones en dirección a Andalucía, sembrando el temor entre los reyes de taifas andaluces.

Almotamid, rey de Sevilla, al saber que Alfonso VI se acercaba, tuvo la idea de enviarle, no un ejército, sino solamente una embajada que habría de pactar con el castellano.

Designó Almotamid para realizar tan difícil misión, a su amigo el poeta Abenamar, que ocupaba el cargo de visir, quien con acompañamiento de un lucido séquito llevando valiosos presentes, salió de Sevilla y encontró junto a Sierra Morena al rey Don Alfonso.

Plantó Abenamar una lujosa tienda de campaña, de rica seda, y convidó al rey de Castilla a que viniera, para ofrecerle un agasajo.

Durante la comida, condimentada con especias y perfumes, según la usanza mora, Abenamar se esforzó en sonsacar a Don Alfonso sus gustos e inclinaciones para saber cómo podría mejor captarse su voluntad. Y habiéndose enterado de que al rey le agradaba mucho el ajedrez, le dijo:

—Si os place, de sobremesa podríamos jugar una partida. Precisamente traigo un lindo tablero de nácar y ébano, y figurillas labradas en marfil, que no las hay mejores en España.

Mucho agradó a Don Alfonso la proposición, pues se tenía por gran jugador, y para demostrarlo, propuso:

—Habremos de jugar apostando algún dinero, pues no es razón que juguemos como las mujeres o los chiquillos.

—Muy puesta en razón es vuestra sugerencia; sin embargo me temo que yo, simple embajador, no tendré dineros para apostarlos en cantidad suficiente para jugar nada menos que contra un rey. Sin embargo os propongo una apuesta más sencilla. Si os gano me daréis dos granos de trigo por el primer cuadro del tablero, cuatro granos por el segundo, dieciséis por el tercero, y así multiplicando el número por sí mismo a cada escaque. Si yo pierdo os daré igual.

Hízole gracia a Don Alfonso la forma de jugar, y más cuando Abenamar le indicó que tenía un pequeño terreno, y que con el trigo que pensaba ganarle podría sembrar su parcela cuando llegase el otoño.

Sin embargo Abenamar estaba preparándole un ingenioso ardid a Don Alfonso VI con el propósito de salvar a Sevilla.

Jugaron, pues, la partida, y perdió Don Alfonso. Sonriendo, dijo:

—Bien, Abenamar, me habéis ganado. Os pagaré lo que apostamos. En cuanto llegue a Castilla daré orden de que os envíen unos cuantos sacos de trigo, y podréis sembrar vuestro campito con buen trigo castellano.

—¿Cómo unos cuantos sacos? Bromeáis, señor. Hagamos la cuenta, pues no quiero recibir ni un solo grano de más, pero tampoco de menos.

Alfonso, de buena gana, y todavía riendo, tomó papel y pluma y empezó a hacer la cuenta. Dos granos por el primer escaque del tablero, cuatro por el segundo, dieciséis por el tercero.

Pero a medida que iban siendo más escaques, la cifra, siempre multiplicada por sí misma, iba alcanzando unas cantidades que escapaban a todo lo imaginable. La progresión era tal, que cuando llegaban a menos de la mitad del tablero, ya no había posibilidad de operar, y para completar el tablero no habría trigo en todos los graneros de Castilla, al que cada año pagaba un impuesto o parias, a cambio había empeñado su palabra de rey, y le era imposible el cumplirla.

En tal situación, abatido y confuso el rey castellano, Abenamar le propuso:

—Señor, pues que la pérdida es tan grande y no podéis pagarla, yo me daría por satisfecho de condonaros la deuda a cambio de que retiraseis vuestro ejército fuera de las fronteras de mi señor el rey Almotamid de Sevilla. Y si queréis hacer guerras, dirigir más bien vuestros afanes hacia Badajoz, o hacia Murcia o Granada, cuyos reyes no son vasallos del de Sevilla.

No satisfizo mucho al castellano la solución, pero como no podía tomar otra, hubo de aceptarla, y así, despidiéndose de Abenamar, ordenó la retirada de su ejército hasta la línea fronteriza, tal como el poeta le había pedido.

Así fue cómo gracias a su ingenio, a su habilidad en el juego del ajedrez, y a su conocimiento de las matemáticas, pudo Abenamar salvar a Sevilla.

En un artículo del Diario ABC, se recoge la misma historia, y se sitúa la leyenda en el año 1078.

Figura 2

 
Además del exquisito ambiente romántico y caballeresco que tiene esta leyenda, nos ha llamado mucho la atención su contenido matemático, que vamos a estudiar a continuación.

En el relato hemos resaltado en negrita la propuesta de Abenamar, que volvemos a reproducir aquí: "Si os gano me daréis dos granos de trigo por el primer cuadro del tablero, cuatro granos por el segundo, dieciséis por el tercero, y así multiplicando el número por sí mismo a cada escaque". Se trata de una sucesión de números en la que cada término se obtiene multiplicando por sí mismo el anterior:

En el primer escaque: 2
En el segundo escaque: 2 · 2 = 4
En el tercer escaque: 4 · 4 = 16

Si continuamos la sucesión iremos obteniendo:

En el cuarto escaque: 16 · 16 = 256
En el quinto escaque: 256 · 256 = 65536
En el sexto escaque: 65536 · 65536 = 4294967296
En el séptimo escaque: 4294967296 · 4294967296 = 18446744073709551616, etc.

Si conocemos la leyenda del inventor del ajedrez, que se puede leer en una entrada de este blog, nos daremos cuenta rápidamente que aunque las leyendas son parecidas, las sucesiones de granos sobre los escaques del tablero son muy diferentes.

En la leyenda del inventor del ajedrez, la sucesión de granos era:
1, 2, 4, 8, 16, 32, 64, 128, ...

En nuestra leyenda de hoy entre Abenamar y Alfonso VI, la sucesión de granos sobre los escaques es:
2, 4, 16, 256, 65536, 4294967296, 18446744073709551616, ...

Una cosa que salta a la vista comparando ambas sucesiones es que en la sucesión de Abenamar aparecen de forma inmediata números ENORMES. En efecto, la primera sucesión crece de forma mucho más suave y lenta que la segunda, y esta última tiene un crecimiento brutalmente acelerado.

De hecho, podemos comprobar que esta segunda sucesión está formada por las potencias de 2 con exponente igual a los términos de la primera sucesión:

2¹ = 2
2² = 4
2⁴ =16
2⁸ = 256
2¹⁶ = 65536
2³² = 4294967296
2⁶⁴ = 18446744073709551616, etc.

Si seguimos avanzando en los escaques, podemos comprobar que en el último escaque el número de granos de trigo sería:

2^{9223372036854775808} = ?

¿Cuánto puede ser esta cantidad? No es un trabajo fácil hacerse una idea de este número. Si por ejemplo tratamos de calcularlo con la calculadora científica que aparece en la página Web2.0calc, la respuesta que nos sale es directamente "infinity".

Con la ayuda de los logaritmos, podemos hacer una aproximación en potencias de 10 o notación científica:

2^{9223372036854775808} ≈ 1.38 · 10^{2776511644261678566}   (*)

Como se puede ver, se trata de una cifra del orden de un 1 seguido de más de dos trillones de ceros. Este número es grande, pero ¿cuánto de grande? Recordemos que un gúgol es 10 elevado a 100, es decir, un 1 seguido de 100 ceros. Un gúgol es un número enorme; los astrofísicos han calculado que el número de partículas subatómicas que existen en nuestro universo visible no va mucho más allá de 10 elevado a 80. Pero el número que hay en la última casilla del tablero de Abenamar es MUCHO, pero MUCHÍSIMO más grande, es 10 elevado a 2.7 trillones.

Si queremos verlo desde otro punto de vista, regresemos a los primeros escaques del tablero. En el séptimo escaque, el número de granos se dispara a los 18 trillones (que es casi exactamente el número de granos TOTALES que cabían en el tablero completo de ajedrez de la primera leyenda). Si calculamos el octavo, el noveno y el décimo escaque:

2¹²⁸ ≈ 3.4 · 10³⁸
2²⁵⁶ ≈ 1.15 · 10⁷⁷
2⁵¹² ≈ 1.34 · 10¹⁵⁴

Es decir, en el décimo escaque habría que poner una cantidad en granos de trigo superior a un 1 seguido de 154 ceros. Si cada partícula del universo visible se transformara en grano de trigo, no habría suficiente trigo en todo el universo para llenar el décimo escaque. Y todavía faltarían por rellenar el undécimo escaque, el duodécimo, etc., hasta el número 64.

Y eso no es todo. Además habría que sumar todos los granos de los 64 escaques. Sin embargo, en este caso no tiene demasiada importancia. Cuando el número de granos crece, hay tanta diferencia entre un escaque y el siguiente que la suma total de granos es muy poco mayor que la cantidad de granos que hay en el último escaque, el número que hay en (*).

Para terminar quisiéramos hacer un último comentario: por lo que se cuenta en la leyenda, creemos que el narrador no tiene una idea ni siquiera aproximada de las cifras que aparecen en la sucesión de Abenamar. En la leyenda se dice literalmente que "... A medida que iban siendo más escaques, la cifra, siempre multiplicada por sí misma, iba alcanzando unas cantidades que escapaban a todo lo imaginable. La progresión era tal, que cuando llegaban a menos de la mitad del tablero, ya no había posibilidad de operar..."

Si tenemos en cuenta que en aquella época había que hacer las cuentas a mano, y que en Europa todavía se seguían utilizando los números romanos, es muy improbable que el rey Alfonso VI pasara de la séptima casilla, que ya alcanza los cuatro mil millones, y que ya implica una multiplicación de dos números de cinco cifras. Intentar calcular la octava casilla es ya una tarea muy larga y complicada a mano, incluso con nuestro sistema decimal, y las demás casillas se tornan prácticamente imposibles. No sólo no podemos llegar a la mitad del tablero (32 casillas), sino que nos quedamos muy lejos de dicha mitad, como mucho sólo es calculable a mano la primera de las filas.

[Créditos de las imágenes: la Figura 1 es un retoque de una imagen tomada de la página web Mercado Libre Argentina, y la Figura 2 ha sido tomada del artículo periodístico publicado en ABC.]

El papel doblado que llega hasta el final del Universo

Cuaderno de bitácora: uno de esos días, pensando en las musarañas, me vino al recuerdo esa paradoja que afirma que doblando un papel muchas veces podemos conseguir el grosor que queramos. Aparece, por ejemplo, en el libro de Adrián Paenza, Matemática... ¿Estás ahí?, y en muchos otros sitios.

Por centrarnos en una fuente, en la web de Gizmodo aparece un artículo de Carlos Zahumenszky titulado Si doblas un papel 103 veces será más grueso que el Universo. Concretamente, expone el artículo:

La leyenda urbana dice que es imposible doblar una hoja de papel por la mitad más de ocho veces. En realidad, el récord mundial lo tiene Britney Gallivan, con 12 pliegues. Lo fascinante es que, según las matemáticas, si doblamos un papel por la mitad 103 veces, su grosor sería mayor que el diámetro del Universo observable, estimado en 93.000 millones de años luz.

La explicación a esta deliciosa paradoja está en el crecimiento exponencial. Una hoja de papel normal (el típico formato A4 con un gramaje de 80 gm /m²) tiene un grosor de 0,1 milímetros. Si la doblamos exactamente por la mitad, tendremos el doble de ese grosor.

A medida que la sigamos doblando una y otra vez por la mitad las cosas se ponen interesantes (e imposibles). Doblada siete veces, la hoja tiene un grosor equivalente a un cuaderno. Si la pudiéramos doblar 23 veces, su grosor ya superaría el kilómetro. 30 pliegues nos llevarían al espacio, sobrepasando la barrera de los 100 kilómetros. En 42 pliegues llegaríamos a la luna, y en 52 al sol.

El grosor del papel sigue aumentando exponencialmente. En 81 pliegues, su grosor sería casi el de la galaxia de Andrómeda, con 127 años luz. Solo 9 pliegues más llevarían a nuestro papel imaginario más allá de los confines del Supercluster de Virgo en el que nuestra galaxia convive con al menos otras cien.

Llegamos al papel doblado 103 veces. Su grosor sería superior a 93.000 millones de años luz.

En el artículo hemos resaltado en negrita o cursiva algunos detalles, pues con su ayuda queremos comentar y puntualizar esta paradoja.

Figura 1. El Universo observable representado en escala logarítmica. La imagen es de Pablo Carlos Budassi y está tomada de la wikipedia.

Es correcto decir que las matemáticas nos aportan las herramientas necesarias para estudiar el problema, como el crecimiento exponencial. En efecto, si vamos doblando en cada paso el grosor del papel, no se necesitan muchos pasos (103 pasos en total según los cálculos del artículo) para ir de un grosor de tan solo 0,1 milímetros, a un grosor superior al tamaño del Universo. Hagamos los cálculos para comprobar que es así:

0,1 · 2¹⁰³ = 1014120480182583521197362564300,8 milímetros

Dividimos por 1.000.000 y nos da:

= 1.014.120.480.182.583.521.197.362 kilómetros aproximadamente

Dividimos por 300.000 · 3600 · 24 · 365 = 9.460.800.000.000 para pasar esta distancia a años-luz y nos da:

= 107.191.831.576 años-luz aproximadamente, un poco mayor que 93.000 millones de años-luz.

Llegar y superar el tamaño del Universo conforme doblamos el grosor de papel es idealmente posible, pero no es posible hacerlo mediante dobleces de un simple folio A4. Si empleamos la lógica y las matemáticas nos podemos dar cuenta rápidamente que la tarea es imposible si no se tiene una hoja de papel de tamaño adecuado.

Por un lado debemos destacar algo obvio: si doblamos un papel por la mitad, el grosor aumenta al doble, pero el tamaño del papel se reduce a la mitad. Por otro lado, cada doblez se hace curvando el papel, y la longitud del papel se emplea también en rodear la curva del doblez. Véase, por ejemplo, el siguiente gráfico:

Figura 2.

En la zona D se acumula el papel doblado, pero además tenemos a un lado y otro capas de dobleces en forma semicircular. La longitud de la hoja de papel se ha ido distribuyendo en todas estas capas, gastándose según el grosor del papel, y de esta forma queda limitado el número de dobleces que se pueden hacer por la propia longitud o tamaño del papel.

La primera persona que, de forma documentada, estableció esta limitación del número de dobleces fue Britney Gallivan, en 2001. No sólo argumentó esta limitación, sino que además obtuvo una fórmula que daba exactamente la relación entre la longitud del papel, L, el grosor t, y el número de dobleces n. Como conclusión a su estudio y demostración práctica de su fórmula, tomó un papel suficientemente largo y lo dobló 12 veces.

Como ilustración de nuestra entrada, traducimos a continuación el artículo de la Historical Society of Pomona Valley, publicado el 3 de abril del 2005:

DOBLANDO PAPEL POR LA MITAD 12 VECES

Britney Gallivan ha resuelto el Problema de Doblar Papel. Este bien conocido desafío consistía en doblar papel a la mitad más de siete u ocho veces, usando papel de cualquier tamaño o forma.

En abril de 2005, el éxito de Britney fue mencionado en el show televisivo de la CBS Numb3rs, en hora de máxima audiencia.

Para conseguir créditos extra para una clase de matemáticas, a Britney le plantearon el desafío de doblar cualquier cosa 12 veces. Después de experimentar de forma exhaustiva, dobló una lámina de oro 12 veces, rompiendo el récord. Lo hizo usando direcciones alternadas de doblado. El desafío se redefinió para doblar un papel. Britney estudió el problema y fue la primera persona en darse cuenta de la causa básica de los límites, y entonces dedujo la fórmula del límite de doblado para cualquier tamaño. Se dedujeron fórmulas de límite para el caso de doblar en direcciones alternadas y para el caso de doblar en una sola dirección usando una larga tira de papel. Las ventajas de cada forma de doblar son discutibles, pero para un alto número de dobleces, el doblado en una sola dirección requiere menos papel.

Se dedujo el límite exacto para el caso del doblado en una sola dirección. Se basa en los efectos limitantes acumulados por cada uno de los dobleces durante el proceso. Si consideramos la complejidad del problema, la fórmula tiene un aspecto relativamente simple.

Para el caso de doblado en una sola dirección, la fórmula exacta del límite es:

 (1)

donde L es la longitud mínima posible del material, t es el grosor del material, y n es el número de dobleces posibles en una dirección. L y t deben expresarse en las mismas unidades.

El doblado en direcciones alternas tiene el siguiente límite:

Esta fórmula da la anchura W de la pieza cuadrada de papel que se necesita para doblarla n veces, en direcciones alternas. La fórmula completa del doblado alterno es compleja, pero esta fórmula relativamente simple nos da una cota que no puede excederse y está bastante cerca del límite exacto.

Para papel no cuadrado, la anterior fórmula da un límite ajustado. Si el papel tiene una proporción entre el largo y el ancho de 2:1, podemos imaginar que lo doblamos una vez y así comienza con un grosor del doble del original, y entonces usamos la fórmula anterior, recordando que debemos añadir el primer doblado.

Britney definió reglas y definiciones estrictas para el proceso de doblado. Una regla es: Para que una hoja se considere doblada n veces debe documentarse convincentemente y verificarse independientemente que 2ⁿ capas únicas descansan en al menos una línea recta. Las secciones que no cumplen este criterio no se cuentan como parte de la sección doblada.

En algunas páginas web, los límites encontrados por Britney son descritos como debidos a la relación entre el grosor y la anchura de los dobleces finales, o atribuídos a que la persona que dobla no es suficientemente fuerte para doblar más veces. Ambas explicaciones para los límites matemáticos son incorrectas y no dan con la auténtica razón detallada para el límite físico-matemático.

En un solo día Britney fue la persona en conseguir el récord de doblar papel a la mitad en 9, 10, 11 y 12 veces.

Algunos hablan equivocadamente de humedecer el papel para conseguir más dobleces, estrujar la hoja de papel como una guía de teléfonos para dividir a la mitad su grosor, o estirar el papel húmedo o seco. Humedecer el papel sólo consigue que se rasgue más fácilmente. Rasgar y cortar no es doblar.

Figura 3. Britney Gallivan sobre el doblez número 11, antes de efectuar el doblez número 12.

Bien, si usamos la fórmula (1) obtenida por Britney Gallivan y queremos tener realmente un papel que doblado alcance el grosor del universo visible, entonces haciendo cuentas:

L = π · 0,1 · (2¹⁰³ + 4) · (2¹⁰³ − 1) / 6 ≅ 5,385 · 10⁶⁰ milímetros

Si esta cantidad la dividimos entre 1.000.000 para pasarla a kilómetros, y entre 9.460.800.000.000 para pasarla a años-luz, nos da aproximadamente 5,69 · 10⁴¹ años-luz. Si comparamos esta enorme cantidad con la anchura del universo, 93.000 millones de años-luz, entonces tenemos aproximadamente:

6.120.218.381.123.657.274.171.314.576.586,2 ≅ 6 quintillones

Resumiendo: según la fórmula de Gallivan, si queremos doblar un papel hasta que su grosor alcance el ancho de nuestro universo observable, debemos doblarlo sobre sí mismo 103 veces, y esto sólo sería posible con un papel de grosor 0,1 milímetros si tuviera una longitud superior a 6 quintillones de veces la anchura de nuestro universo.

Por otro lado, si queremos doblar 12 veces un papel de grosor 0,1 milímetros, como hizo Britney Gallivan en 2001, debemos tomar una tira de papel cuya longitud sea por lo menos mayor que:

L = π · 0,1 · (2¹² + 4) · (2¹² − 1) / 6 ≅ 879.096 milímetros, es decir, un poco más de 879 metros.

Lo único que nos resta es hacer el experimento.

Notas: el número 2¹⁰³ = 10.141.204.801.825.835.211.973.625.643.008 está mencionado en nuestra entrada Potencias de dos, pues se acerca mucho a una potencia de 10, concretamente a 10³¹ (diez quintillones), y apenas se separa de este número un 1,4%.

Referencias: la figura 2 es una adaptación de la imagen que aparece en la página de la Historical Society of Pomona Valley conservada en el Internet Archive, que relata el trabajo de Britney Gallivan.

Cómo resolver las Torres de Hanói

Cuaderno de bitácora: gracias a la guía de nuestro compañero matenavegante Pablo Viedma, un día pudimos visitar, en nuestro periplo mateoceánico, las Torres de Hanói.

Este juego fue inventado en el año 1883 por un matemático francés, Edouard Lucas. Se trata de un solitario que se compone de tres pivotes o estacas verticales insertadas en un tablero y una pila con un cierto número de discos de tamaños crecientes, normalmente siete u ocho.

Figura 1.

El juego consiste en trasladar la pila entera de discos de uno de los pivotes a cualquiera de los otros dos, pero teniendo en cuenta las reglas:

-Sólo se puede tomar un disco en cada movimiento.
-El disco tiene que estar en la posición superior de su pila.
-Al pasarlo a otro pivote no se puede colocar sobre otro disco más pequeño.

Edouard Lucas, para dar mayor interés y contexto al juego, se inventó la leyenda de que el juego se había creado en un templo de Benarés, en la India, hoy ya desaparecido. Según esa leyenda, allí se comenzó con una Torre de 64 discos apilados.

Es fácil calcular el número mínimo de movimientos necesarios para trasladar toda la torre de una varilla a otra: 2ⁿ − 1, siendo n el número de discos que hay en la torre.

Si por ejemplo tenemos una torre de 8 discos, como en la figura 1, el número mínimo de movimientos será de:

2⁸ − 1 = 256 − 1 = 255 movimientos.

En el caso de la leyenda del templo de Benarés, para mover toda la torre de 64 discos de un pivote a otro, se necesitarían:

2⁶⁴ − 1 = 18.446.744.073.709.551.615 movimientos como mínimo, más de 18 trillones.

Con un sencillo cálculo se puede comprobar que si hiciéramos un movimiento por segundo harían falta 584.942.417.355 años para completar todo el traslado.

El número total de movimientos para 64 discos nos recuerda otra leyenda famosa en matemáticas, la del inventor del ajedrez. Se dice que cuando el inventor presentó el ajedrez a su rey, este le ofreció como premio cualquier cosa que pidiera. El inventor pidió un grano de trigo por la primera casilla del tablero de ajedrez, dos granos de trigo por la segunda casilla, cuatro por la tercera, ocho por la cuarta, y así sucesivamente, doblando la cantidad de granos en cada casilla hasta completar las 64 de todo el tablero. Si calculamos el número de granos de trigo que hay que reunir en total nos sale exactamente la misma cantidad que los movimientos de la torre de 64 discos:

2⁶⁴ - 1 = 18.446.744.073.709.551.615 granos de trigo. (Para más información, consultar la entrada Leyenda sobre el tablero de ajedrez)

Hay estudios matemáticos muy completos sobre las Torres de Hanói. Es realmente interesante conocer la relación que existe entre las posiciones de los discos y los números del sistema binario. Otra actividad muy interesante para los grumetes es investigar en qué movimiento se mueve cada disco, y obtener así diversas progresiones aritméticas. Quizás dediquemos entradas futuras a tratar estos dos aspectos.

Pero enfrentémonos al juego e intentemos resolverlo. Nos daremos cuenta de que si los discos son muy pocos, dos, tres, hasta cuatro, trasladar la torre es sencillo. Pero a partir de cinco, seis discos... la cosa se empieza a poner complicada, el número de movimientos crece rápidamente y es muy fácil perderse.

Para ello hay dos trucos, cualquiera de los dos ayudan por separado a resolver el puzle, y si los combinamos entonces no podemos perdernos.

-El primer truco consiste en pintar los discos en dos colores diferentes, alternados, por ejemplo blanco y negro. También debemos pintar las bases de los pivotes en colores alternados: los pivotes libres uno debe ser negro de base y el otro blanco, y el pivote de partida debe tener el color contrario al disco más grande. Cuando tengamos pintados los discos y las bases debemos añadir una nueva regla: cada disco que movamos debe colocarse sobre otro disco o base de color contrario, nunca del mismo color.

-El segundo truco consiste en fijarse en que  el disco más pequeño, el que inicialmente está en la cúspide de la torre, se mueve en el movimiento 1º, 3º, 5º, 7º, 9º, ... en todos los movimientos impares. Empezamos moviendo el disco pequeño, movemos otro disco, luego otra vez el pequeño, luego otro disco, luego el pequeño otra vez, luego otro disco, luego el pequeño, y así sucesivamente. De cada dos discos que movemos, uno es el pequeño.

Además, siempre debemos mover el disco pequeño en el mismo sentido. Entre los pivotes hay dos sentidos de movimiento: el que podemos llamar sentido positivo o de izquierda a derecha, 1→2→3→1, y el que podemos llamar sentido negativo o de derecha a izquierda, 3→2→1→3.

Vamos a emplear este segundo truco o procedimiento para resolver este solitario. Haremos el ejemplo de una torre con 4 discos.

Figura 2.

A continuación ponemos la secuencia completa de 2⁴ − 1 = 15 movimientos:

movimiento 1º: a1 → 2
movimiento 2º: b1 → 3
movimiento 3º: a2 → 3
movimiento 4º: c1 → 2
movimiento 5º: a3 → 1
movimiento 6º: b3 → 2
movimiento 7º: a1 → 2
movimiento 8º: d1 → 3
movimiento 9º: a2 → 3
movimiento 10º: b2 → 1
movimiento 11º: a3 → 1
movimiento 12º: c2 → 3
movimiento 13º: a1 → 2
movimiento 14º: b1 → 3
movimiento 15º: a2 → 3

Veamos los movimientos en una secuencia de fotografías:

Figura 3.
 a1 → 2

Figura 4.
 b1 → 3

Figura 5.
a2 → 3

Figura 6.
c1 → 2

Figura 7.
a3 → 1

Figura 8.
b3 → 2

Figura 9.
a1 → 2

Figura 10.
d1 → 3

Figura 11.
a2 → 3

Figura 12.
b2 → 1

Figura 13.
a3 → 1

Figura 14.
c2 → 3

Figura 15.
a1 → 2

Figura 16.
b1 → 3

Figura 17.
a2 → 3 y final.

Obsérvese que:

-El disco más pequeño, el a, siempre se ha movido de izquierda a derecha y en los movimientos impares, es decir, cada 2 movimientos.
-El segundo disco, el b, se ha movido de derecha a izquierda; se movió en el 2º movimiento y luego cada 4 movimientos (en el 6º, el 10º y el 14º).
-El tercer disco, el c, se ha movido como el a, de izquierda a derecha, empezando en el 4º movimiento y luego cada 8 movimientos (en el 12º).
-El cuarto disco, el d, se ha movido como el b, de derecha a izquierda, empezando en el 8º movimiento y luego le tocaba moverse cada 16 movimientos, pero como en nuestro ejemplo no había más que 15 movimientos, este disco sólo se ha movido una vez.

Con este ejemplo creemos que el lector puede guiarse para resolver el pasatiempo cuando la torre tiene más discos, aunque conforme el número de discos aumenta, el número de movimientos aumenta exponencialmente, y es difícil no perder la atención y confundirse en cualquier momento.

El Triángulo de Sierpinski en pop-up

Cuaderno de bitácora: Hace años, cuando nuestro periplo nos llevaba por los matemares de Priego de Córdoba, aprendimos una construcción con papel y tijeras que queremos presentar aquí, para deleite de nuestros "numerosos" seguidores: el pop-up del Triángulo de Sierpinski.

(Entiéndase la palabra numerosos en sentido estricto matemático: hay un número de seguidores de nuestro blog, no importa si ese número es grande o pequeño, y menos importa en matemáticas, donde un número tan grande como un gúgol está tan cerca del infinito como el número uno.)

Recordamos en las siguientes imágenes qué es el triángulo de Sierpinski:

Tomamos un triángulo (en negro) y lo "agujereamos" quitando el triángulo central que conecta los puntos medios de los lados, obtenemos tres triángulos (negros) semejantes al primero, ahora volvemos a agujerear esos tres triángulos, y obtenemos nueve triángulos, volvemos a agujerearlos y así vamos iterando el proceso hasta el infinito.

El resultado es un fractal llamado Triángulo de Sierpinski.
[Imagen realizada por Beojan Stanislaus.]

Bien, si ya estamos provistos de un folio A4 y de unas tijeras, podemos empezar a construir nuestro pop-up o relieve en papel. También son muy útiles una regla, un lápiz y una goma. Sigamos la secuencia de fotografías para saber cómo se debe proceder.

Figura 1.
Se dobla el folio por la mitad. El rectángulo formado vamos a llamarlo escalera de 1 peldaño. Cortamos desde la mitad del doblez hasta la mitad del peldaño.

Figura 2.
Doblamos la parte de arriba, haciendo coincidir el borde del rectángulo pequeño con el borde izquierdo del folio.
Remarcamos el doblez.

Figura 3.
Desdoblamos e invertimos el doblez, introduciendo el rectángulo entre las dos caras del folio.
Con esto ya tenemos la escalera de 2 peldaños.

Figura 4.
Aquí tenemos una vista desde arriba de la escalera de 2 peldaños, formando ya una estructura tridimensional.

Figura 5.
Otra vista de la misma escalera, donde se aprecia el hueco formado por los dobleces interiores.

Figura 6.
En el siguiente paso cortamos cada uno de los dos peldaños por la mitad hasta el centro del rectángulo, tal como se indica en la imagen.

Figura 7.
Doblamos los rectángulos superiores a los cortes.

Figura 8.
Procedemos a invertir los dobleces, empujando los peldaños hacia el interior del papel, y obtenemos la escalera de 4 peldaños.

Figura 9.
Este es el resultado, en forma de pop-up tridimensional, de la escalera de 4 peldaños.

Figura 10.
Continuamos haciendo otra iteración o repetición del mismo proceso.

Figura 11.
Hacemos los dobleces formando los nuevos peldaños.

Figura 12.
Esta es la forma tridimensional en este tercer paso de la escalera de 8 peldaños. 

Figura 13.

Figura 14.
Conforme aumentan los peldaños, el número de dobleces también aumenta, de forma exponencial. Ya estamos en una escalera de 16 peldaños.

Figura 15.
La escalera de 16 peldaños. La forma tridimensional se va pareciendo cada vez más al triángulo de Sierpinski.

Figura 16.
Continuamos con la quinta iteración. 

Figura 17.
Hemos conseguido la escalera de 32 peldaños.
Invertir los dobleces de esta escalera es un trabajo meticuloso que lleva un buen rato de esfuerzo y paciencia.

Figura 18.
El resultado final.

Con un folio A4, el máximo objetivo es la escalera de 32 peldaños y el pop-up de la figura 18. Llegar hasta este paso requiere bastante paciencia. Suponemos que es posible hacer una escalera de 64 peldaños, pero imaginamos que ya es un trabajo para especialistas en miniaturas, en busca de batir récords, y no digamos de 128 peldaños. También se puede empezar por hojas más grandes, de tamaño A3, A2 o incluso más grandes.

Hay que tener en cuenta que el número de dobleces interiores que tenemos que realizar, se multiplica por 3 en cada paso. Para la primera escalera tuvimos que invertir 1 doblez, para la segunda 3, para la tercera 9, para la cuarta 27 y para la quinta 81. Si quisiéramos conseguir la escalera de 64 peldaños nos esperan nada más y nada menos que 243 inversiones de dobleces más.

Leyenda sobre el tablero de ajedrez

Entre todas las versiones que he leído sobre la invención del ajedrez, la que voy a transcribir a continuación es la que más me ha gustado, pues su ambientación logra trasladarme al encantado mundo de las mil y una noches.

Esta versión aparece en el libro Matemáticas recreativas de Yakob Perelman [traducción de F. Blanco y C. Pérez, Ediciones Martínez Roca].

El juego del ajedrez fue inventado en la India. Cuando el rey hindú Sheram lo conoció, quedó maravillado de lo ingenioso que era y de la variedad de posiciones que en él son posibles. Al enterarse de que el inventor era uno de sus súbditos, el rey lo mandó llamar con objeto de recompensarle personalmente por su acertado invento.

Figura 1

El inventor, llamado Seta, se presentó ante el soberano. Era un sabio vestido con modestia, que vivía gracias a los medios que le proporcionaban sus discípulos.

-Seta, quiero recompensarte dignamente por el ingenioso juego que has inventado -dijo el rey.

El sabio contestó con una inclinación.

-Soy bastante rico como para poder cumplir tu deseo más elevado -continuó diciendo el rey-. Di la recompensa que te satisfaga y la recibirás.

Seta continuó callado.

-No seas tímido -le animó el rey-. Expresa tu deseo. No escatimaré nada para satisfacerlo.

-Grande es tu magnanimidad, soberano. Pero concédeme un corto plazo para meditar la respuesta. Mañana, tras maduras reflexiones, te comunicaré mi petición.

Cuando al día siguiente Seta se presentó de nuevo ante el trono, dejó maravillado al rey con su petición, sin precedente por su modestia.

-Soberano -dijo Seta-, manda que me entreguen un grano de trigo por la primera casilla del tablero de ajedrez.

-¿Un simple grano de trigo? -contestó admirado el rey.

-Sí, soberano. Por la segunda casilla, ordena que me den dos granos; por la tercera, 4; por la cuarta, 8; por la quinta, 16; por la sexta, 32... 

Figura 2

-Basta -le interrumpió irritado el rey-. Recibirás el trigo correspondiente a las 64 casillas del tablero de acuerdo con tu deseo: por cada casilla doble cantidad que por la precedente. Pero has de saber que tu petición es indigna de mi generosidad. Al pedirme tan mísera recompensa, menosprecias, irreverente, mi benevolencia. En verdad que, como sabio que eres, deberías haber dado mayor prueba de respeto ante la bondad de tu soberano. Retírate. Mis servidores te sacarán un saco con el trigo que solicitas.

Seta sonrió, abandonó la sala y quedó esperando a la puerta del palacio.

Durante la comida, el rey se acordó del inventor del ajedrez y envió a que se enteraran de si habían ya entregado al irreflexivo Seta su mezquina recompensa.

-Soberano, están cumpliendo tu orden -fue la respuesta-. Los matemáticos de la corte calculan el número de granos que le corresponden.

El rey frunció el ceño. No estaba acostumbrado a que tardaran tanto en cumplir sus órdenes.

Por la noche, al retirarse a descansar, el rey preguntó de nuevo cuánto tiempo hacía que Seta había abandonado el palacio con su saco de trigo.

-Soberano -le contestaron-, tus matemáticos trabajan sin descanso y esperan terminar los cálculos al amanecer.

-¿Por qué va tan despacio este asunto? -gritó iracundo el rey-. Que mañana, antes de que me despierte, hayan entregado a Seta hasta el último grano de trigo. No acostumbro a dar dos veces la misma orden.

Por la mañana comunicaron al rey que el matemático mayor de la corte solicitaba audiencia para presentarle un informe muy importante.

El rey mandó que le hicieran entrar.

-Antes de comenzar tu informe -le dijo Sheram-, quiero saber si se ha entregado por fin a Seta la mísera recompensa que ha solicitado.

-Precisamente por eso me he atrevido a presentarme tan temprano -contestó el anciano-. Hemos calculado escrupulosamente la cantidad total de granos que desea recibir Seta. Resulta una cifra tan enorme...

-Sea cual fuere su magnitud -le interrumpió con altivez el rey- mis graneros no empobrecerán. He prometido darle esa recompensa, y por lo tanto, hay que entregársela.

-Soberano, no depende de tu voluntad el cumplir semejante deseo. En todos tus graneros no existe la cantidad de trigo que exige Seta. Tampoco existe en los graneros de todo el reino. Hasta los graneros del mundo entero son insuficientes. Si deseas entregar sin falta la recompensa prometida, ordena que todos los reinos de la Tierra se conviertan en labrantíos, manda desecar los mares y océanos, ordena fundir el hielo y la nieve que cubren los lejanos desiertos del Norte. Que todo el espacio sea totalmente sembrado de trigo, y ordena que toda la cosecha obtenida en estos campos sea entregada a Seta. Sólo entonces recibirá su recompensa.

El rey escuchaba lleno de asombro las palabras del anciano sabio.

-Dime cuál es esa cifra tan monstruosa -dijo reflexionando.

-¡Oh, soberano! Dieciocho trillones cuatrocientos cuarenta y seis mil setecientos cuarenta y cuatro billones setenta y tres mil setecientos nueve millones quinientos cincuenta y un mil seiscientos quince.

Hasta aquí la leyenda. A continuación, algunos comentarios matemáticos.

La leyenda de la invención del ajedrez nos ilustra sobre el rápido crecimiento de una progresión geométrica (de razón mayor que la unidad). En este caso tenemos una progresión geométrica en la que la razón es 2, pues cada término de la progresión es el doble del anterior.

La sucesión de términos es: 1, 2, 4, 8, 16, 32,... Obsérvese que esta sucesión coincide con las potencias de dos: 2⁰, 2¹, 2², 2³, 2⁴, 2⁵,...

El término general de la progresión, la fórmula que nos da cada número, es: aₙ = 2ⁿ⁻¹.

En la última casilla hay exactamente: 2⁶³ = 9.223.372.036.854.775.808 (un poco más de 9 trillones) granos de trigo.

El número de granos de trigo totales se calcula sumando todos los términos: 1 + 2 + 4 + 8 + ... Esto se hace más sencillamente gracias a la fórmula de la suma de los términos de una progresión geométrica:

Como curiosidad, si añadimos un grano más de trigo a la suma, obtenemos la siguiente potencia de 2: 2⁶⁴ = 18.446.744.073.709.551.616. Esto es debido a que conforme vamos sumando los granos de cada casilla, siempre nos quedamos a un solo grano de la casilla siguiente:

1 + 2 = 3 = 4 − 1
1 + 2 + 4 = 7 = 8 − 1
1 + 2 + 4 + 8 = 15 = 16 − 1, etc.

Todos estos números, 1, 3, 7, 15, etc., son llamados números de Mersenne. Se llama número de Mersenne a cualquier número anterior a una potencia positiva de 2, más concretamente a los números de la forma Mₙ = 2ⁿ − 1, con n ≥ 1.

Un aspecto interesante que merece la pena reflexionar es el comentario del matemático mayor del rey Sheram, cuando le explica que el número de granos de trigo es una cifra monstruosa. Pienso, y puedo estar equivocado, que cuando uno de nosotros lee la cifra, le parece simplemente una cifra grande, pero no tiene realmente idea de lo grande que es. De hecho, los granos de trigo son cosas de un tamaño muy pequeño, y en un saco de trigo puede haber muchísimos granos, aunque no sabemos cuántos.

Debemos tener en cuenta que cualquiera de nosotros, en nuestra época actual, hemos oído hablar de muchos ejemplos de cifras monstruosas: la población mundial, el producto interior bruto de un país desarrollado, la edad del universo, el número de estrellas que hay en la Vía Láctea, el número de kilómetros que equivale a un año-luz, el número de moléculas que hay en un mol de una sustancia (número de Avogadro), el gúgol, etc. Si con la imaginación nos trasladamos a la mitológica época del rey Sheram, a la India de los Vedas, a los inicios del sistema numérico decimal que ahora tenemos, podemos comprender que ya el mismo hecho de calcular, a mano, números tan grandes, debía suponer un enorme esfuerzo para los matemáticos de la época, que debían estar acostumbrados a contabilidades prácticas con números mucho más manejables.

Para hacerse una idea de lo grande que es la cantidad de 18 trillones de granos de trigo, hay que convertirla a una unidad más manejable, gramos, kilogramos o toneladas de trigo, y compararla con la producción de trigo mundial. Se pueden encontrar muchas páginas que hacen esta conversión, pero curiosamente hay discrepancia entre ellas.

En la wikipedia (en español), por ejemplo, hay una estimación de unos 1200 granos de trigo por kilogramo, con lo que cada grano de trigo pesaría casi un gramo, (lo cual me parece exagerado). Según dicha estimación, tomando toda la producción mundial actual de trigo, se necesitarían más de 22000 años para acumular los 18 trillones de granos pedidos por el inventor Seta.

La página de wikipedia en inglés, estima que cada grano de trigo pesa 0,065 gramos, lo cual equivale a que en un kilo hay unos 15000 granos de trigo, y calcula que el total de trigo del tablero de ajedrez es más de 1600 veces la producción mundial.

En Matemáticas cercanas, la estimación es de unos 25000 granos de trigo por kilo, es decir, cada grano de trigo pesaría 0,04 gramos. Según este cálculo, se necesitarían más de 1000 años para acumular los granos del tablero de ajedrez.

En la página de SMPM y en la de Me llevo las Mates de calle, se estima que un grano de trigo pesa 0,03 gramos, lo cual hace que en un kilo quepan unos 33000 granos de trigo, y que se necesiten unos 800 años para completar el pedido.

En cualquier caso, si aceptamos que para completar el pedido del inventor Seta se necesita aproximadamente la producción mundial de trigo durante 1000 años, ya sí nos podemos hacer una idea de lo monstruosa que es la cifra calculada por los matemáticos del rey Sheram.

Créditos de las imágenes:

Figura 1: extraída de Collectors Weekly.

Figura 2: By McGeddon [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons.

Una moneda para un sorteo

Cuaderno de bitácora: en relación con la situación que se dio en cierto colegio de Granada, en la que se explica lo erróneo del método empleado por algunos Directores para realizar sorteos de plazas escolares, podemos reflexionar qué se puede necesitar para hacer un sorteo probabilísticamente justo con los mínimos elementos posibles.

Cuando se estudia probabilidad, ¿cuál es el ejemplo más simple que se pone de experimento aleatorio? Suele ser el lanzamiento de una moneda. Cuando echamos una moneda al aire, al caer puede quedar expuesta una de sus dos caras (cara o cruz), tenemos, por tanto, dos sucesos elementales posibles C = cara, X = cruz.

Pero repitiendo el lanzamiento, obtenemos combinaciones de sucesos elementales que nos pueden ayudar, por ejemplo, a realizar un sorteo justo con la ayuda de tan solo una moneda.

Tomemos el ejemplo que tratábamos en el caso del sorteo de las plazas escolares. Se trata de elegir aleatoriamente un número entre 111 posibilidades. ¿Se puede hacer con la exclusiva ayuda de una moneda?

La idea es ir tomando el conjunto de números, y dividirlo en dos partes iguales, asignar C a una de las partes y X a la otra, y luego lanzar la moneda para quedarnos con una de las mitades. A esta mitad la dividimos a su vez en dos partes y volvemos a asignar C a una parte, y X a la otra, y así sucesivamente, hasta que nos quedemos solamente con un número, que será el número elegido.

Pero 111 no se puede dividir en dos conjuntos iguales, porque es un número impar, y luego debemos seguir dividiendo por dos varias veces.

Necesitamos utilizar potencias de dos; las potencias de dos con exponente un número entero positivo son: 2, 4, 8, 16, 32, 64, 128, 256, etc.

Para el ejemplo que tenemos nos basta tomar 128. Cogemos pues 128 números. Como en realidad los alumnos son 111, del 112 al 128 los números corresponden a alumnos ficticios, o por decirlo de otra manera, si al final del sorteo tenemos la mala suerte de que es elegido uno de estos alumnos ficticios, el sorteo queda anulado y se vuelve a repetir desde el principio.

Tomamos estos 128 números, los dividimos en dos partes iguales de 64 cada una, del 1 al 64 y del 65 al 128. Si sale C, nos quedaremos con la primera mitad, si sale X con la segunda.

Lanzamos la moneda, nos sale, por ejemplo, X, y nos quedamos con los números del 65 al 128 (son 64 números en total). Volvemos a dividir el grupo en dos partes iguales, de 32 números; si sale C nos quedamos con los números del 65 al 96, si sale X, con los números del 97 al 128.

Lanzamos la moneda y nos sale en este segundo intento X otra vez, nos quedamos con los números del 97 al 128.

Así podemos seguir: dividimos el grupo en dos mitades, del 97 al 112, del 113 al 128; lanzamos la moneda y nos sale C, nos quedamos con la primera mitad.

Dividimos otra vez: del 97 al 104, del 105 al 112; lanzamos y sale C, nos quedamos con la primera mitad.

Dividimos: del 97 al 100, del 101 al 104; lanzamos y sale X.

Dividimos: del 101 al 102, del 103 al 104; lanzamos y sale C.

Ahora nos quedan solo dos números, el 101 y el 102; lanzamos y sale C. Nuestro número elegido es el 101.

La sucesión XXCCXCC nos ha llevado al número 101.

Cualquier matenavegante un poco curtido está observando que este método se relaciona íntimamente con los números binarios. En efecto, la sucesión XXCCXCC se puede trasladar de forma natural a número binario con sólo sustituir las X por 1 y las C por 0.

XXCCXCC → 1100100

Sin embargo, si convertimos nuestro número binario en número decimal, parece que las cuentas no coinciden:

1100100 = 1 · 2⁶ + 1 · 2⁵ + 0 · 2⁴ + 0 · 2³ + 1 · 2² + 0 · 2¹ + 0 · 2⁰ = 64 + 32 + 4 = 100.

Sin embargo el número elegido no es 100, sino 101, ¿por qué esta discrepancia?

Si nosotros tomamos los números binarios de siete cifras desde 0000000 a 1111111, en sistema decimal estos números representan del 0 al 127. En nuestro sorteo hemos considerado los números del 1 al 128. Es decir, es como si tomáramos la lista de números binarios de siete cifras y la desplazáramos un lugar, por lo tanto la conversión en caras y cruces a números binarios debe hacerse sumando una unidad al resultado:

XXCCXCC = 1100100 + 1 = 100 + 1 = 101

Con este ejemplo podemos ver que se puede realizar un sorteo justo aunque no se disponga más que de una moneda. Siempre que la moneda no esté trucada.