Uno de esos textos habla sobre el gúgol y el gúgolplex (googol y googolplex en inglés). Los matenavegantes suelen conocer estos dos números, ya que han ido adquiriendo cierta fama a lo largo del tiempo.
Un gúgol es un número: un 1 seguido de cien ceros. En potencias de diez, diríamos que es diez elevado a cien, 10100. Es, por tanto, un número muy grande, enorme.
Un
millón es un 1 seguido de seis ceros, un
billón (en España) es un 1 seguido de 12 ceros. Un
trillón, un 1 seguido de dieciocho ceros. Éstos ya son números muy grandes. El gúgol es mucho, mucho, pero mucho más grande que cualquiera de los mencionados. En la
definición de gúgol de la Wikipedia, que recomendamos leer porque trae unas cuantas curiosidades sobre el gúgol, se comenta, por ejemplo, que siguiendo la misma tónica de potencias de diez: trillón, cuatrillón, quintillón, sextillón, septillón, octillón, etc., el gúgol equivaldría a
diez mil hexadecillones.
Un gúgol, como hemos dicho, es enorme, pero mucho peor es el gúgolplex. El gúgolplex es otro número: un 1 seguido de un gúgol de ceros, o en potencias de diez, diríamos diez elevado a un gúgol.
La ocurrencia de ponerle nombres propios a estos dos números la tuvo Milton Sirotta, el sobrino de nueve años del matemático americano Edward Kasner. En el libro
Matemáticas e Imaginación, de Edward Kasner y James Newman, se dice, por ejemplo, que
Palabras de sabiduría pronuncian los niños, por lo menos tan a menudo como los hombres de ciencia. El nombre "gúgol" fue inventado por un niño (sobrino del doctor Kasner, de nueve años de edad), a quien se le pidió que propusiera un nombre para un número muy grande, a saber: un 1 seguido de cien ceros. Estaba muy seguro de que este número no era infinito y, por lo tanto, igualmente en lo cierto de que tenía que tener un nombre. Al mismo tiempo que indicó la palabra "gúgol", sugirió el nombre para otro número aún mayor: "gúgolplex". Un gúgolplex es mucho mayor que un gúgol, pero continúa siendo finito, como se apresuró a señalar el inventor de su nombre. Primero se sugirió que un gúgolplex sería un 1 seguido de tantos ceros que uno se cansase de escribirlos. Esto es una descripción de lo que sucedería si uno tratara realmente de escribir un gúgolplex, pero distintas personas se cansan en tiempos diferentes y no consideraríamos a Carnera [un boxeador de la época] mejor matemático que al doctor Einstein, sencillamente porque tuviera más resistencia. El gúgolplex es, pues, un número finito determinado, formado por tantos ceros después de la unidad, que el número de ceros sea igual a un gúgol.
En otro pasaje del mismo libro, se dice también que
Desgraciadamente, tan pronto como la gente habla de números grandes, pierde la chaveta. Parecen hallarse bajo la impresión de que, ya que cero es igual a nada, pueden agregar a un número tantos ceros como les plazca sin que ello traiga consecuencias serias. Tendremos que ser un poco más cuidadosos, pues, al hablar de números grandes.
En efecto, corroborando lo que dice el libro, una vez que explicamos a los grumetes lo que significa un gúgol, ellos no parecen captar la idea. No les culpamos, porque es muy raro que alguien pueda captar la idea al principio. Les decimos, por ejemplo, que se ha calculado el número de partículas subatómicas del universo (protones, neutrones, electrones, fundamentalmente) y que ese número es menor que un gúgol, está en torno a diez elevado a ochenta, o un 1 seguido de ochenta ceros. Les decimos también que si quisiéramos escribir un gúgolplex, no habría en el universo espacio suficiente para escribir todos los ceros. Parece que con estas comparaciones es suficiente para que capten el concepto, pero no es así.
Porque de repente, siempre surge la misma ocurrencia: ¿y tener tanto dinero como un gúgol?
Hasta ahora no me había dado cuenta que una de las mejores maneras para hacerse una idea de los números grandes es hablar en términos de dinero. Ahí los grumetes, y cualquier persona, en general, tiene muchas referencias, y además interesantes, porque es fácil suponer que tenemos grandes cantidades de dinero y dejar volar la imaginación con todo lo que podríamos hacer con ellas.
Si hablamos de mil euros, por ejemplo, estamos hablando del sueldo mensual, un poco bajo, de una persona (últimamente se ha acuñado el término mileurista para designar en España a los trabajadores que tienen un sueldo en torno a mil euros al mes, cantidad que es escasa a la hora de hacer frente a la hipoteca de un piso, el mantenimiento de una familia, etc.) Si hablamos de diez mil euros, entonces ya entramos en lo que vale, por ejemplo, un automóvil sencillo. Si fueran cien mil euros, es el valor de un piso pequeño en una ciudad donde los precios de los pisos sean bajos.
Cuando llegamos a un millón de euros, entonces ya nos podemos imaginar una casa grande con jardín, piscina, bien amueblada, y si son diez millones de euros, empezamos a movernos en las cifras que ganan algunos deportistas al año. Cien millones de euros es un poco más de lo que costó el traspaso de Cristiano Ronaldo al Real Madrid, y puede ser el presupuesto de una superproducción de Hollywood protagonizada por actores famosos. Miles de millones de euros se pueden usar para contabilizar la fortuna de algunos multimillonarios. Aquí ya se empieza a perder la perspectiva.
Un billón de euros, (un millón de millones), es una cifra que se usa en la economía global de los países. El Producto Interior Bruto (PIB) en España, la suma de todos los bienes y servicios finales producidos en un año, fue en 2008 alrededor de un billón de euros, mientras que el PIB mundial, es decir, la suma de todos los países, no llegó a cincuenta billones de euros.
Un mil billones de euros, por tanto, es más de lo que se ha producido en todo el mundo durante los veinte últimos años.
Si ahora subimos a un trillón de euros (un 1 seguido de dieciocho ceros), resulta que es más de mil veces el dinero que se ha movido en todo el mundo en veinte años, ¿qué se le puede decir a un grumete cuando con ingenua e inconciente ocurrencia pregunta por un gúgol de euros?
En ese momento clave intento contestarle de forma contundente, y mi propia imaginación me traiciona. Lo primero que digo es que ese dinero no existe, que no hay tanto dinero en el mundo, y el grumete me pregunta: ¿por qué?
Luego se me ocurre decirle que con ese dinero se podría comprar el mundo entero, qué digo el mundo, el sistema solar entero, y esto último ya me parece bastante fuerte.
Pero poco a poco lo realmente enorme de tal cantidad se va abriendo paso en mi mente: un gúgol de euros...
No hay un gúgol de partículas subatómicas en el universo, luego si se me ocurriera pagar un euro por cada átomo del universo, podría comprar el universo entero, y me sobraría mucho dinero...
Pagar un euro por cada átomo es un precio CARÍSIMO. ¡Para comprar un SIMPLE vaso de agua no habría suficiente dinero en el mundo!.
Si yo tuviera un gúgol de euros, podría pagar un euro por cada átomo y comprar este universo entero.
Si yo tuviera un gúgol de euros, podría pagar un euro por cada partícula subatómica y comprar un trillón de universos como éste...
Si yo tuviera un gúgol de euros...

































 Dice Sam Griffiths-Jones en su Introducción al Nurikabe:
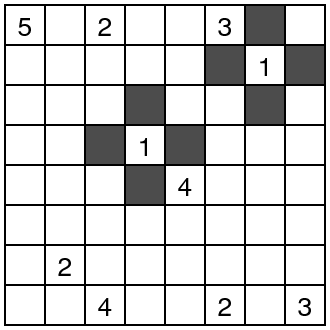
Dice Sam Griffiths-Jones en su Introducción al Nurikabe: