Entre todas las versiones que he leído sobre la invención del ajedrez, la que voy a transcribir a continuación es la que más me ha gustado, pues su ambientación logra trasladarme al encantado mundo de las mil y una noches.
Esta versión aparece en el libro Matemáticas recreativas de Yakob Perelman [traducción de F. Blanco y C. Pérez, Ediciones Martínez Roca].
Esta versión aparece en el libro Matemáticas recreativas de Yakob Perelman [traducción de F. Blanco y C. Pérez, Ediciones Martínez Roca].
El juego del ajedrez fue inventado en la India. Cuando el rey hindú Sheram lo conoció, quedó maravillado de lo ingenioso que era y de la variedad de posiciones que en él son posibles. Al enterarse de que el inventor era uno de sus súbditos, el rey lo mandó llamar con objeto de recompensarle personalmente por su acertado invento.
 |
| Figura 1 |
El inventor, llamado Seta, se presentó ante el soberano. Era un sabio vestido con modestia, que vivía gracias a los medios que le proporcionaban sus discípulos.
-Seta, quiero recompensarte dignamente por el ingenioso juego que has inventado -dijo el rey.
El sabio contestó con una inclinación.
-Soy bastante rico como para poder cumplir tu deseo más elevado -continuó diciendo el rey-. Di la recompensa que te satisfaga y la recibirás.
Seta continuó callado.
-No seas tímido -le animó el rey-. Expresa tu deseo. No escatimaré nada para satisfacerlo.
-Grande es tu magnanimidad, soberano. Pero concédeme un corto plazo para meditar la respuesta. Mañana, tras maduras reflexiones, te comunicaré mi petición.
Cuando al día siguiente Seta se presentó de nuevo ante el trono, dejó maravillado al rey con su petición, sin precedente por su modestia.
-Soberano -dijo Seta-, manda que me entreguen un grano de trigo por la primera casilla del tablero de ajedrez.
-¿Un simple grano de trigo? -contestó admirado el rey.
-Sí, soberano. Por la segunda casilla, ordena que me den dos granos; por la tercera, 4; por la cuarta, 8; por la quinta, 16; por la sexta, 32...
Figura 2
-Basta -le interrumpió irritado el rey-. Recibirás el trigo correspondiente a las 64 casillas del tablero de acuerdo con tu deseo: por cada casilla doble cantidad que por la precedente. Pero has de saber que tu petición es indigna de mi generosidad. Al pedirme tan mísera recompensa, menosprecias, irreverente, mi benevolencia. En verdad que, como sabio que eres, deberías haber dado mayor prueba de respeto ante la bondad de tu soberano. Retírate. Mis servidores te sacarán un saco con el trigo que solicitas.
Seta sonrió, abandonó la sala y quedó esperando a la puerta del palacio.
Durante la comida, el rey se acordó del inventor del ajedrez y envió a que se enteraran de si habían ya entregado al irreflexivo Seta su mezquina recompensa.
-Soberano, están cumpliendo tu orden -fue la respuesta-. Los matemáticos de la corte calculan el número de granos que le corresponden.
El rey frunció el ceño. No estaba acostumbrado a que tardaran tanto en cumplir sus órdenes.
Por la noche, al retirarse a descansar, el rey preguntó de nuevo cuánto tiempo hacía que Seta había abandonado el palacio con su saco de trigo.
-Soberano -le contestaron-, tus matemáticos trabajan sin descanso y esperan terminar los cálculos al amanecer.
-¿Por qué va tan despacio este asunto? -gritó iracundo el rey-. Que mañana, antes de que me despierte, hayan entregado a Seta hasta el último grano de trigo. No acostumbro a dar dos veces la misma orden.
Por la mañana comunicaron al rey que el matemático mayor de la corte solicitaba audiencia para presentarle un informe muy importante.
El rey mandó que le hicieran entrar.
-Antes de comenzar tu informe -le dijo Sheram-, quiero saber si se ha entregado por fin a Seta la mísera recompensa que ha solicitado.
-Precisamente por eso me he atrevido a presentarme tan temprano -contestó el anciano-. Hemos calculado escrupulosamente la cantidad total de granos que desea recibir Seta. Resulta una cifra tan enorme...
-Sea cual fuere su magnitud -le interrumpió con altivez el rey- mis graneros no empobrecerán. He prometido darle esa recompensa, y por lo tanto, hay que entregársela.
-Soberano, no depende de tu voluntad el cumplir semejante deseo. En todos tus graneros no existe la cantidad de trigo que exige Seta. Tampoco existe en los graneros de todo el reino. Hasta los graneros del mundo entero son insuficientes. Si deseas entregar sin falta la recompensa prometida, ordena que todos los reinos de la Tierra se conviertan en labrantíos, manda desecar los mares y océanos, ordena fundir el hielo y la nieve que cubren los lejanos desiertos del Norte. Que todo el espacio sea totalmente sembrado de trigo, y ordena que toda la cosecha obtenida en estos campos sea entregada a Seta. Sólo entonces recibirá su recompensa.
El rey escuchaba lleno de asombro las palabras del anciano sabio.
-Dime cuál es esa cifra tan monstruosa -dijo reflexionando.
-¡Oh, soberano! Dieciocho trillones cuatrocientos cuarenta y seis mil setecientos cuarenta y cuatro billones setenta y tres mil setecientos nueve millones quinientos cincuenta y un mil seiscientos quince.
Hasta aquí la leyenda. A continuación, algunos comentarios matemáticos.
La leyenda de la invención del ajedrez nos ilustra sobre el rápido crecimiento de una progresión geométrica (de razón mayor que la unidad). En este caso tenemos una progresión geométrica en la que la razón es 2, pues cada término de la progresión es el doble del anterior.
La sucesión de términos es: 1, 2, 4, 8, 16, 32,... Obsérvese que esta sucesión coincide con las potencias de dos: 2⁰, 2¹, 2², 2³, 2⁴, 2⁵,...
El término general de la progresión, la fórmula que nos da cada número, es: aₙ = 2ⁿ⁻¹.
En la última casilla hay exactamente: 2⁶³ = 9.223.372.036.854.775.808 (un poco más de 9 trillones) granos de trigo.
El número de granos de trigo totales se calcula sumando todos los términos: 1 + 2 + 4 + 8 + ... Esto se hace más sencillamente gracias a la fórmula de la suma de los términos de una progresión geométrica:
Como curiosidad, si añadimos un grano más de trigo a la suma, obtenemos la siguiente potencia de 2: 2⁶⁴ = 18.446.744.073.709.551.616. Esto es debido a que conforme vamos sumando los granos de cada casilla, siempre nos quedamos a un solo grano de la casilla siguiente:
1 + 2 = 3 = 4 − 1
1 + 2 + 4 = 7 = 8 − 1
1 + 2 + 4 + 8 = 15 = 16 − 1, etc.
Todos estos números, 1, 3, 7, 15, etc., son llamados números de Mersenne. Se llama número de Mersenne a cualquier número anterior a una potencia positiva de 2, más concretamente a los números de la forma Mₙ = 2ⁿ − 1, con n ≥ 1.
Un aspecto interesante que merece la pena reflexionar es el comentario del matemático mayor del rey Sheram, cuando le explica que el número de granos de trigo es una cifra monstruosa. Pienso, y puedo estar equivocado, que cuando uno de nosotros lee la cifra, le parece simplemente una cifra grande, pero no tiene realmente idea de lo grande que es. De hecho, los granos de trigo son cosas de un tamaño muy pequeño, y en un saco de trigo puede haber muchísimos granos, aunque no sabemos cuántos.
Debemos tener en cuenta que cualquiera de nosotros, en nuestra época actual, hemos oído hablar de muchos ejemplos de cifras monstruosas: la población mundial, el producto interior bruto de un país desarrollado, la edad del universo, el número de estrellas que hay en la Vía Láctea, el número de kilómetros que equivale a un año-luz, el número de moléculas que hay en un mol de una sustancia (número de Avogadro), el gúgol, etc. Si con la imaginación nos trasladamos a la mitológica época del rey Sheram, a la India de los Vedas, a los inicios del sistema numérico decimal que ahora tenemos, podemos comprender que ya el mismo hecho de calcular, a mano, números tan grandes, debía suponer un enorme esfuerzo para los matemáticos de la época, que debían estar acostumbrados a contabilidades prácticas con números mucho más manejables.
Para hacerse una idea de lo grande que es la cantidad de 18 trillones de granos de trigo, hay que convertirla a una unidad más manejable, gramos, kilogramos o toneladas de trigo, y compararla con la producción de trigo mundial. Se pueden encontrar muchas páginas que hacen esta conversión, pero curiosamente hay discrepancia entre ellas.
En la wikipedia (en español), por ejemplo, hay una estimación de unos 1200 granos de trigo por kilogramo, con lo que cada grano de trigo pesaría casi un gramo, (lo cual me parece exagerado). Según dicha estimación, tomando toda la producción mundial actual de trigo, se necesitarían más de 22000 años para acumular los 18 trillones de granos pedidos por el inventor Seta.
La página de wikipedia en inglés, estima que cada grano de trigo pesa 0,065 gramos, lo cual equivale a que en un kilo hay unos 15000 granos de trigo, y calcula que el total de trigo del tablero de ajedrez es más de 1600 veces la producción mundial.
En Matemáticas cercanas, la estimación es de unos 25000 granos de trigo por kilo, es decir, cada grano de trigo pesaría 0,04 gramos. Según este cálculo, se necesitarían más de 1000 años para acumular los granos del tablero de ajedrez.
En la página de SMPM y en la de Me llevo las Mates de calle, se estima que un grano de trigo pesa 0,03 gramos, lo cual hace que en un kilo quepan unos 33000 granos de trigo, y que se necesiten unos 800 años para completar el pedido.
En cualquier caso, si aceptamos que para completar el pedido del inventor Seta se necesita aproximadamente la producción mundial de trigo durante 1000 años, ya sí nos podemos hacer una idea de lo monstruosa que es la cifra calculada por los matemáticos del rey Sheram.
Créditos de las imágenes:
Figura 1: extraída de Collectors Weekly.
Figura 2: By McGeddon [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons.

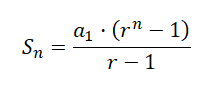




No hay comentarios:
Publicar un comentario