Regla de este Sudoku: llenar las casillas vacías de forma que en cada
fila, en cada columna y en cada caja de 3×3 estén todas las letras del
siguiente conjunto:
30.6.21
Sudoku de letras (31)
26.6.21
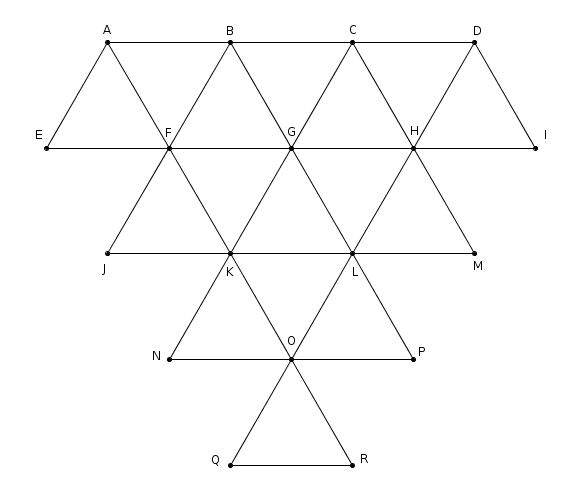
[El Problema de la Semana] Más Triángulos de un Solo Trazo
Continuando con el trazado de grafos sin levantar el lápiz del papel, proponemos al lector el siguiente:
¿Sería capaz el lector de dibujar de un solo trazo el siguiente grafo lleno de triángulos?
Más abajo encontrará la solución.
 |
| Esta fotografía está tomada en el Centro de Conferencias KAFD en Riyadh, Arabia Saudita. El autor del diseño es Daniel Buren, un artista conceptual francés. La imagen está sacada de este sitio. |
SOLUCIÓN:
El recorrido se puede hacer de muchas formas. A continuación exponemos una de las posibles soluciones, la cual me fue sugerida por un grumete del Barco Escuela:
A-E-F-J-K-N-O-Q-R-O-K-F-A-B-F-G-K-L-O-P-L-G-B-C-G-H-L-M-H-C-D-H-I-D
También exponemos otra solución, con un recorrido un poco más complejo:
A-E-F-G-H-I-D-H-L-O-Q-R-O-K-F-A-B-C-G-K-N-O-P-L-G-B-F-J-K-L-M-H-C-D
AMPLIACIÓN:
Como se ha explicado en el problema de la semana anterior, Triángulos de un Solo Trazo, Euler demostró que un grafo era resoluble mediante un solo trazo siempre que el número de vértices impares fuera cero o dos, pero no es resoluble si el número de vértices impares es cuatro o más.
En nuestro ejemplo de hoy tenemos que todos los vértices son pares, salvo el A y el D. Luego este grafo es resoluble, siempre que tomemos A y D como puntos de inicio y final.
Nota: este problema está inspirado en uno de los capítulos del libro Mathematics and the Imagination, de Edward Kasner y James Newman.
23.6.21
Sudoku de letras (30)
Regla de este Sudoku: llenar las casillas vacías de forma que en cada
fila, en cada columna y en cada caja de 3×3 estén todas las letras del
siguiente conjunto:
19.6.21
[El Problema de la Semana] Triángulos de un Solo Trazo
Presentamos hoy uno de los típicos problemas o pasatiempos en los que hay que conseguir trazar una figura de un solo trazo, es decir, en una sola línea, sin levantar el lápiz del papel y sin pasar dos veces por un mismo camino ya dibujado:
¿Es usted capaz de dibujar, de un solo trazo, la siguiente figura triangulada?
La solución, unos cuantos triángulos más abajo.
SOLUCIÓN:
En este grafo en particular podemos empezar a trazar por cualquiera de los puntos, y si hacemos el recorrido de forma inteligente lograremos nuestro objetivo.
Así, por ejemplo, podemos empezar por el vértice A, y luego hacer el siguiente recorrido:
A - C - D - B - G - I - J - H - E - C - F - I - H - F - D - G - F - E - A
Pasando en este orden por los diferentes vértices habremos resuelto el problema. Hay muchas otras soluciones que el lector puede ir probando.
AMPLIACIÓN:
Históricamente, el problema de dibujar grafos pasando por todas las aristas sin levantar el lápiz del papel tiene su origen en el Problema de los Puentes de Königsberg. Este problema fue resuelto por Leonhard Euler, y dio origen a una nueva rama de las matemáticas, la Topología, también llamada originalmente Analisis Situs.
La solución de Euler es muy sencilla de entender y se basa en clasificar los vértices del grafo en vértices pares o impares, según el número de aristas que convergen en cada vértice:
-Si un grafo solo tiene vértices pares, entonces se puede dibujar de un solo trazo, empezando por cualquier vértice.
-Si un grafo tiene dos vértices impares y el resto son pares, también se puede dibujar, pero esta vez hay que empezar el trazo en uno de los vértices impares, mientras que el otro vértice impar será el punto en el que finaliza el trazo.
-Si un grafo tiene cuatro o más vértices impares, entonces no se puede dibujar de un solo trazo.
En el grafo que hemos puesto en el problema de hoy, podemos ver que todos los vértices son pares: en A, B y J convergen 2 aristas, en C, D, E, G, H e I convergen 4 aristas, y en F convergen 6. Por tanto, se puede dibujar de un solo trazo, empezando por cualquier punto.
Nota: este problema está inspirado en un capítulo del libro Mathematics and the Imagination, de Edward Kasner y James Newman.
16.6.21
Newton and Leibniz - Newton y Leibniz
Newton and Leibniz
Sir Isaac Newton (1643-1727) was an English mathematician and scientist who is generally thought to be one of the greatest mathematicians of all time. He identified the principle of gravitation and the fact that it applied to all bodies throughout the Universe, establishing a formula to predict its effect in all circumstances. He formulated the three laws of motion and, by using a prism, established that white light was made up or a spectrum of colours. One of his greatest achievements was the invention of the calculus.
Gottfried von Leibniz (1646-1716) was a German mathematician who, independently of Newton, but about the same time, also invented the calculus. Though their methods were the same in principle, they differed widely in the notation they used. Controversy over which was the better dragged on for almost a century, but it is the Leibniz notation we use today.
Newton y Leibniz
Sir Isaac Newton (1643-1727) fue un matemático y científico inglés que generalmente se piensa que es uno de los más grandes matemáticos de todos los tiempos. Identificó el principio de gravitación y el hecho de que se aplicaba a todos los cuerpos del Universo, estableciendo una fórmula para predecir su efecto en todas las circunstancias. Formuló las tres leyes del movimiento y, con el uso de un prisma, estableció que la luz blanca estaba compuesta de un espectro de colores. Uno de sus grandes logros fue la invención del cálculo (*).
Gottfried von Leibniz (1646-1716) fue un matemático alemán, que independientemente de Newton, pero sobre la misma fecha, también inventó el cálculo.
Aunque sus métodos eran en principio los mismos, se diferenciaban mucho
en la notación que usaron. La controversia sobre cuál era la mejor, se
mantuvo durante casi un siglo, pero es la notación de Leibniz la que usamos hoy.
(*) A la rama matemática desarrollada por Newton y Leibniz, en inglés se le ha dado el nombre de calculus, pero en español la palabra cálculo tiene la acepción general de "cómputo que se hace de algo por medio de operaciones matemáticas". Por tanto, una traducción más específica de calculus sería cálculo infinitesimal, y también análisis matemático.
Nota: el texto en inglés ha sido extraído y adaptado del libro Oxford Study Mathematics Dictionary.
12.6.21
[El Problema de la Semana] El Espía de la Trinchera de Color Ocre
Cuaderno de bitácora: hoy transcribimos un problema de lógica, ambientado en la época de los espías:
EL ESPÍA DE LA TRINCHERA DE COLOR OCRE
Un misterio en doce puntos
por SUSAN ZIVICH
1. Cuatro espías con trinchera se habían acomodado en asientos encarados.
2. Viajaban en el exprés de Pekín.
3. Dos iban junto a la ventanilla, y los otros dos al lado del pasillo.
4. La colocación resultaba un tanto extraña (como sin duda pensó el lector).
5. El espía inglés estaba sentado a la izquierda del señor B.
6. El señor A llevaba una trinchera beige.
7. El espía con trinchera de color oliva se hallaba a la derecha del espía alemán.
8. El señor C era el único que fumaba un puro.
9. El señor D estaba en frente del espía norteamericano.
10. El ruso, vestido de caqui, llevaba una bufanda al cuello.
11. El espía inglés miraba por la ventanilla, a su izquierda.
12. ¿Quién era el espía de la trinchera de color ocre?
La solución: en la página 144 y más abajo.
 |
| Este problema ha sido extraído de un número de la revista Selecciones del Reader's Digest, concretamente del publicado en octubre de 1979 en España. El mismo problema, aunque con el texto de la edición de Ecuador, también ha sido publicado en el blog Momento Digital. La palabra trinchera apenas se utiliza hoy en la acepción en la que la vemos en este problema. Si miramos la acepción 3 del Diccionario de la Real Academia de la Lengua Española, trinchera es una "gabardina de aspecto militar". |
SOLUCIÓN:
Necesitamos hacernos un esquema con los asientos, la ventanilla y el pasillo. El problema ya traía un dibujo que parece facilitar la situación.
El problema tiene algunos puntos que no aportan información relevante y tan solo sirven para ambientarlo. Por ejemplo, en el punto 2 se dice que viajaban en el exprés de Pekín, pero igualmente podría ser un tren que lleva a Moscú, o a Estocolmo, pues eso no aporta información al problema. El punto 8 habla del señor C que fumaba un puro, pero igualmente podría estar bebiendo una limonada, lo único que es útil es saber que hay un señor C.
Teniendo en cuenta esto, vamos a ir extrayendo la información de los diferentes puntos.
Por el punto 11, sabemos que el espía inglés está en el asiento V2.
Por el punto 5, sabemos que el señor B está en el asiento P2.
En el punto 7 se nos habla de que "el espía con trinchera de color oliva se hallaba a la derecha del espía alemán", esto significa que el espía alemán debe estar en el asiento V2 o en el P1, pero el V2 está ocupado por el espía inglés. Por tanto el espía alemán está en P1, y el espía con trinchera de color oliva está en V1.
Por el punto 10, el ruso, vestido de caqui y con una bufanda al cuello (esto último es un dato irrelevante), tiene que encontrarse en P2, y es el señor B.
Por el punto 9, el espía norteamericano debe estar en V1 y tiene trinchera de color oliva. El espía inglés, por tanto, es el señor D.
Por el punto 6, el señor A, que leva una trinchera beige tiene que ser el espía alemán del asiento P1, ya que no puede ser el norteamericano, pues este lleva una trinchera de color oliva.
Ya tenemos que: el ruso viste de color caqui, el alemán viste de color beige y el norteamericano viste de color oliva.
Por eliminación, el espía de la trinchera de color ocre es el inglés.
Nota: como ya se ha indicado, este problema ha sido extraído de la revista Selecciones del Reader's Digest, concretamente del número de octubre de 1979, edición española.
9.6.21
The Platonic solids - Los sólidos platónicos
The Platonic solids
Plato (427-347 BC) identified five polyhedral solids with all faces the same. He associated these with the basic elements which he believed made up the physical world. These Platonic solids are the triangular pyramid (tetrahedron), cube (hexahedron), octahedron, dodecahedron and icosahedron. Plato claimed that earth was made of cubic particles, fire of pyramids, air of octahedrons and water of icosahedrons. He claimed, '… the gods used the dodecahedron for arranging the constellations on the whole heaven'.
In his Elements, Euclid gives a thorough account of the Platonic solids and repeats Plato's assertion that there are only five regular solids.
Los sólidos platónicos
Platón (427-347 a.C.) identificó cinco sólidos poliédricos con todas las caras iguales. Los asoció con los elementos básicos que creía que formaban el mundo físico. Estos sólidos platónicos son la pirámide triangular (tetraedro), el cubo (hexaedro), el octaedro, el dodecaedro y el icosaedro. Platón afirmaba que la tierra estaba hecha de partículas cúbicas, el fuego de pirámides, el aire de octaedros y el agua de icosaedros. Él aseguraba que "... los dioses usaron el dodecaedro para ordenar las constelaciones en todo el cielo".
En sus Elementos, Euclides da una detallada descripción de los sólidos platónicos y repite la afirmación de Platón de que solo hay cinco sólidos regulares.
Nota: el texto en inglés ha sido extraído del libro: The Story of Mathematics, de Anne Rooney.
5.6.21
[El Problema de la Semana] Velocidad de crecimiento
Todavía es primavera:
¿A qué velocidad en kilómetros por hora crece una planta que en seis meses ha pasado de tener 20 centímetros de altura a tener 30?
La solución, 30 centímetros más abajo.
 |
| El problema de hoy nos ha recordado una cuestión similar que aparece en el libro El Hombre Anumérico, de John Allen Paulos. Más abajo, en la ampliación, citamos el texto donde se menciona. La imagen está tomada de la web librosdemario.com. |
SOLUCIÓN:
Se trata de un ejercicio de cambio de unidades.
La velocidad es igual a espacio partido por tiempo. Primero tenemos el espacio:
30 − 20 = 10 centímetros
Lo pasamos a kilómetros:
10 centímetros = 10/100 = 0.1 metros
0.1 metros = 0.1/1000 = 0.0001 kilómetros
Luego tenemos el tiempo:
6 meses = 6 · 30 = 180 días = 180 · 24 = 4320 horas.
Ya podemos calcular la velocidad en kilómetros por hora que nos pide el problema:
velocidad = 0.0001/4320 = 0.000000023148 km/h aproximadamente.
Si ponemos la solución en notación científica, tendríamos: 2.3148 × 10−8 km/h.
AMPLIACIÓN:
Como ya mencionamos en la imagen, este problema es similar a una cuestión que se plantea en el libro El Hombre Anumérico, de John Allen Paulos. Citamos el texto en concreto:
"Siempre me sorprende y me deprime encontrar estudiantes que no tienen la menor idea de cuál es la población de los Estados Unidos, de la distancia aproximada entre las costas Este y Oeste, ni de qué porcentaje aproximado de la humanidad representan los chinos. A veces les pongo como ejercicio que calculen a qué velocidad crece el cabello humano en kilómetros por hora, cuántas personas mueren aproximadamente cada día en todo el mundo, o cuántos cigarrillos se fuman anualmente en el país. Y a pesar de que al principio muestran cierta desgana (un estudiante respondió, simplemente, que el cabello no crece en kilómetros por hora), en muchos casos su intuición numérica acaba mejorando espectacularmente."
Luego continúa más adelante:
"En notación científica, las respuestas a las preguntas que planteé al principio son las siguientes: el cabello humano crece aproximadamente a razón de 1,6 × 10−8 kilómetros por hora; cada día mueren en la tierra unas 2,5 × 105 personas y cada año se fuman aproximadamente 5 × 1011 cigarrillos en los Estados Unidos. Las expresiones de estos números en notación común son: 0,000000016 kilómetros por hora, 250.000 personas y 500.000.000.000 cigarrillos."
Si nos fijamos en la velocidad a la que crece el cabello humano, se parece bastante a la de la hierba de nuestro problema. Concretamente la hierba crece un poco más rápido. ¿Será que con fertilizante para plantas el cabello puede crecer más rápido?
Nota: este problema ha sido extraído del libro Matemágicas, de Ignacio Soret Los Santos.
2.6.21
The Nine Chapters - Los Nueve Capítulos
The Nine Chapters
Los Nueve Capítulos
El texto matemático chino más antiguo, Los Nueve Capítulos del Arte Matemático, apareció por primera vez en el siglo I a.C. Se escribieron muchos comentarios a lo largo de los siglos siguientes, el mejor de los cuales fue de Liu Hui en 263 d.C. El texto demuestra el teorema de Pitágoras (deducido de forma independiente) y enseña como calcular distancias tales como la altura de una torre vista desde una colina, la anchura de un estuario, la altura de una pagoda y la profundidad de un barranco. También trata del cálculo de áreas y volúmenes de figuras como trapezoides, círculos, segmentos de círculos, cilindros, pirámides y esferas.
Nota: el texto en inglés ha sido extraído de The Story of Mathematics, de Anne Rooney.
-
Cuaderno de bitácora: una de las primeras actividades que hemos propuesto a los grumetes durante el inicio del curso en el Barco Escuela, e...
-
Un tema recurrente en los relatos y películas de ciencia ficción son los viajes espaciales. Cruzar las distancias siderales para ir de un pl...
-
Cuaderno de bitácora: en una entrada anterior hicimos la construcción en papel de la llamada Espiral de Fibonacci . Para ello utilizamos ...