Cuaderno de bitácora: recientemente hemos descubierto, gracias al libro Mathematics and the Imagination de Edward Kasner y James Newman, un sencillo hecho que vamos a compartir a continuación.
Nos dan un número cualquiera, x. ¿Sabríamos calcular con regla y compás su raíz cuadrada?
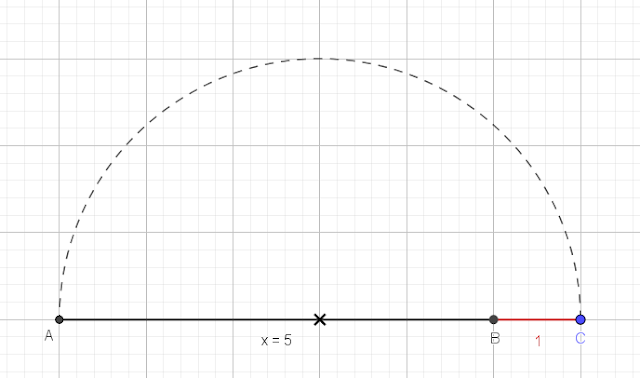
Primero debemos representar gráficamente el número x como un segmento cuya longitud es precisamente x. Vamos a suponer, por ejemplo, que el número es x = 5, y lo representamos gráficamente.
A dicho segmento le añadimos una extensión de longitud 1.
Tomamos ahora el centro del segmento AC y trazamos un semicírculo que pase por A y por C.Levantamos una perpendicular desde el punto B, y la cortamos con el semicírculo. Obtenemos un segmento, AD. La longitud de este segmento es la raíz cuadrada de x. En este caso la raíz cuadrada de 5, que si la aproximamos con decimales sale 2.236067977...
¿Esto funciona siempre así? ¿Cuál es su justificación?
Sí, funciona con cualquier número. Su justificación está en el llamado TEOREMA DE LA ALTURA.
Construimos un triángulo rectángulo. Para ello tomamos como base el lado AC, que va a ser la hipotenusa, y trazamos un semicírculo que pase por A y por C. Elegimos un punto del semicírculo, D, y lo unimos con A y C. Se puede demostrar que el triángulo ACD es rectángulo necesariamente, con el ángulo recto en D y catetos AD y CD.
Desde D trazamos la altura, que corta perpendicularmente a AC en el punto B.
La altura BD corta al triángulo rectángulo original en dos triángulos rectángulos más pequeños, ABD y BCD. Es fácil razonar que los tres triángulos, el grande ACD y los pequeños ABD y BCD son semejantes, ya que sus ángulos son iguales. Por ejemplo, el ángulo A forma parte tanto del triángulo ACD como del ABD, luego estos dos triángulos tienen dos ángulos iguales, el A y el ángulo recto, y por tanto también tienen igual el tercer ángulo, por tanto ACD y ABD son semejantes. Igual razonamiento podemos hacer con el ángulo C, el triángulo ACD y el BCD, y de aquí ACD y BCD también son triángulos semejantes. Como consecuencia, BCD y ABD son semejantes entre sí por ser semejantes ambos al triángulo grande ACD.
Si dos triángulos son semejantes, sus lados correspondientes son proporcionales. Si tomamos los catetos de los triángulos ABD y BCD, entonces se cumple la proporción:
AB/BD = BD/BC
Como en la figura hemos dado los nombres x = AB, y = BC, h = BD, entonces:
x/h = h/y
De aquí, multiplicando en cruz:
h2 = x · y
Este es el teorema de la altura, que dice: "En un triángulo rectángulo, el cuadrado de la altura trazada sobre la hipotenusa es igual al producto de las proyecciones de los catetos sobre la hipotenusa".
En el caso que estamos estudiando en esta entrada, si y = 1, entonces tenemos que
h2 = x ·1 = x
Y por tanto:
h = √x
Así se justifica la construcción que hemos hecho al principio, donde pusimos el ejemplo x = 5.