Cuaderno de bitácora: estamos empezando un nuevo periplo en el Barco Escuela, y este año a los grumetes les hemos propuesto como pasatiempo que aprendan a resolver nurikabes.
Descubrí el Nurikabe en una librería, en la sección de los libros dedicados a juegos y pasatiempos. Entre los libros de sudokus y kakuros estaba El libro del Nurikabe, escrito por Sam Griffith-Jones y publicado por Valor Editions.
 Dice Sam Griffiths-Jones en su Introducción al Nurikabe:
Dice Sam Griffiths-Jones en su Introducción al Nurikabe:
 Dice Sam Griffiths-Jones en su Introducción al Nurikabe:
Dice Sam Griffiths-Jones en su Introducción al Nurikabe:En el folklore japonés, el Nurikabe es una pared invisible que impide al viajero proseguir su camino. El Nurikabe toma la forma de una tabla en la cual están colocados una serie de números. El objetivo es usar esos números para decidir qué casillas en la tabla deberían estar ennegrecidas (el Nurikabe, o pared), y cuales deberían quedarse en blanco, basándose en una serie de normas sencillas. El Nurikabe también es conocido bajo el nombre de "islas en una corriente", donde las casillas negras son la corriente y las casillas blancas las islas. Cada puzzle tiene una sola solución, y siempre se puede llegar a esa solución por deducción lógica. No es menester hacer adivinanzas.
Según la wikipedia, el Nurikabe es un pasatiempo desarrollado por un tal Reenin en el número 33 de la revista Nikoli, publicado en marzo de 1991. Pronto se convirtió en un éxito dentro de la revista, que ha seguido incluyéndolos en todas sus ediciones.
El Nurikabe ha seguido la estela del extraordinario éxito del Sudoku. Después de que el Sudoku se popularizase en 2004, otros pasatiempos de origen japonés han ido apareciendo en todo el mundo. El Kakuro y el Nurikabe son dos de ellos.
En la página web Nurikabe @ Daily Sudoku se explican las reglas, hay un tutorial y una gran colección de nurikabes para imprimir y resolver. Como quiera que la página está en inglés, a continuación incluyo una traducción de las reglas y el tutorial.
Reglas:
-Cada celda o casilla debe ser blanca o negra.
-Cada grupo de casillas blancas (islas) debe contener uno y solo un número.
-El número de casillas blancas en un grupo debe ser igual a ese número.
-Todas las casillas negras deben estar unidas formando un bloque continuo (el muro o corriente).
-Los bloques 2x2 de casillas negras no están permitidos.
Ejemplo resuelto:
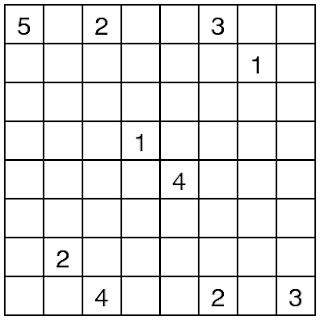
Primer paso: casillas con un 1
Fijémonos en el número 1 cerca del centro de la cuadrícula. Cada isla debe contener un número. El número 1 representa una isla con solo un cuadrado blanco, así que podemos sombrear las casillas adyacentes. Esto mismo es cierto para el 1 de la esquina superior derecha.
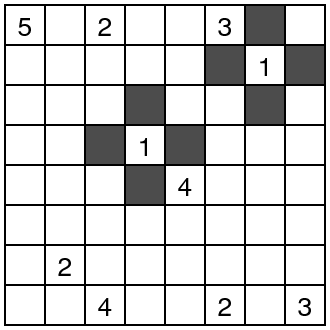
Paso dos: sombreando entre las islas
Ningún grupo de celdas blancas debe contener más de un número. Esto significa que los números deben estar separados por cuadrados negros. Cuando tenemos dos números con un solo cuadrado entre ellos, este cuadrado debe ser ennegrecido. Por ejemplo, el 5 y el 2 de la esquina superior izquierda deben separarse por una casilla negra.

Paso tres: extendiendo el muro
Si nos concentramos en la esquina inferior izquierda de la cuadrícula, cada cuadrado negro debe estar conectado para formar el muro. La casilla negra de la esquina inferior izquierda no debe quedarse aislada. Sólo tiene un cuadrado vecino posible, el cual, por tanto debe ser negro. Donde haya una única posibilidad, debemos extender el muro.

Paso cuatro: extendiendo las islas
Fijémonos en el número 2 en la esquina inferior izquierda. Esta isla no está completa todavía, necesita un segundo cuadrado blanco. El número tiene sólo una casilla vecina posible, y por tanto debe ser blanca. Podemos poner un punto en esa casilla para mostrar que es blanca. Ahora la isla "2" está completa, y por tanto la podemos rodear de cuadrados negros.

Paso cinco: aislamiento
Echemos un vistazo a los cuadrados marcados con (a). Estos cuadrados están rodeados, y por tanto no pueden ser parte de ninguna isla. Se deben sombrear.
Como estamos ahí, debemos extender el muro de la esquina superior derecha. Podemos buscar otros lugares donde el muro debe extenderse también.

Paso seis: otra vez las islas
Miremos el 5 en la esquina superior izquierda. Necesitamos extender la isla. Usemos puntos para señalar los cuadrados que deben ser blancos.
¿Qué otras islas se pueden extender?

Paso siete: bloques 2x2
La última regla dice que no se permiten bloques 2x2. Los dos cuadrados marcados con (a) en la parte central izquierda de la cuadrícula deben ser blancos, porque si los sombreamos violamos dicha regla. Marquémoslos con puntos.

Paso ocho: sombreando entre las islas II
En el paso dos, rellenamos los cuadrados que separaban dos números. Esto lo podemos extender de manera lógica y rellenar los cuadrados que separan las islas que van creciendo. Observemos los cuadrados marcados (a). ¿Se comprende por qué deben ser sombreados?

Paso 9: muro e islas
El error más corriente es concentrarse sólo en el muro, o sólo en las islas. Necesitamos ir cambiando la atención del muro a las islas y de las islas al muro. Busquemos si se pueden extender partes del muro para evitar que se queden aisladas, y extender islas y sombrear las casillas que las rodean cuando están llenas.

Paso 10: ya casi está
¡Casi lo hemos conseguido! Nótese que en la cuadrícula mostrada arriba, debemos rellenar los cuadrados marcados (a) para que no se queden aislados trozos enteros de muro.

Paso 11: últimos cuadrados
Las islas restantes se pueden extender en una sola dirección. El último cuadrado oscuro une dos grandes secciones de muro en una unidad continua.
Paso 12: solución
¡Bien hecho! Obsérvese la distribución de las islas y la línea continua de muro.
En la misma web Nurikabe @ Daily Sudoku hay una página con muchos nurikabes para imprimir.
Notas:
Las reglas del Nurikabe no son tan intuitivas ni tan simples como las de los sudokus. De hecho hay variantes. Así tenemos, que en El libro del Nurikabe, Sam Griffiths-Jones incluye una regla específica, no incluida aquí, que dice que el muro no puede tener ciclos, es decir, el muro no puede contener circuitos cerrados de casillas; otra forma de definir esta misma regla es exigir que dadas dos casillas negras del muro, debe haber un solo camino posible que las une. Además no están permitidos los bloques 2x2 de casillas negras ni tampoco los bloques 2x2 de casillas blancas. Sin embargo, en la página web Nurikabe @ Daily Sudoku no se incluyen estas dos reglas, aunque el ejemplo que trae sí las sigue implícitamente.
Hay otras páginas de Nurikabes en las que los ciclos sí están permitidos explícitamente. Véase, por ejemplo, el siguiente Nurikabe resuelto, que aparece en la página de su.doku.es:

En este Nurikabe hay un ciclo en torno a la isla "1" del centro. Si quisiéramos ir por el muro de una casilla negra que esté junto al 3, a la casilla negra que está junto al 6, habría dos caminos posibles, al poder rodear al 1 central por dos lados distintos.
Hay otras muchas webs en las que aparecen Nurikabes para resolver online. La página de la revista japonesa Nikoli tiene también tutoriales flash (en inglés) para aprender de forma sencilla e interactiva a solucionarlos.





